A. Đúng (theo định nghĩa đạo hàm tại một điểm).
B. Đúng vì:
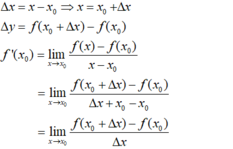
C. Đúng vì:
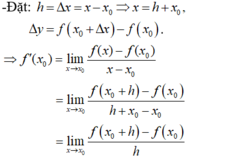
Chọn D
A. Đúng (theo định nghĩa đạo hàm tại một điểm).
B. Đúng vì:
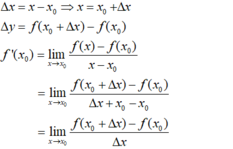
C. Đúng vì:
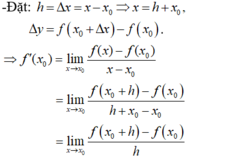
Chọn D
Cho hàm số f ( x ) = x 2 sin 1 x n ế u x ≠ 0 A n ế u x = 0
Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?
Cho hàm số f ( x ) = 3 - 4 - x 4 k h i x ≢ 0 1 4 k h i x = 0 . Khi đó đạo hàm của hàm số tại điểm x = 0 là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R
y = f(x) liên tục trên (−∞;0) và trên [0;+∞) nhưng gián đoạn tại x = 0
Cho hàm số f(x) xác định bởi f ( x ) = x 2 + 1 - x x ( x ≠ 0 ) 0 ( x = 0 ) . Giá trị f’(0) bằng:
A. 0
B. 1
C. 1/2.
D. Không tồn tại.
Cho hàm số f ( x ) = 2 x + 8 - 2 x + 2 K h i x > - 2 0 x = - 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) lim x → 2 + f ( x ) = 0 .
(II) f(x) liên tục tại x = -2
(III) f(x) gián đoạn tại x= -2
A. Chỉ (I) và (III).
B. Chỉ (I) và (II).
C. Chỉ (I).
D. Chỉ (II)
Cho hàm số f ( x ) = 2 x + 8 - 2 x + 2 x > - 2 0 x = - 2 Tìm khẳng định đúng trong các khẳng định sau:
(I) lim x → - 2 + f ( x ) = 0
(II) f(x) liên tục tại x = -2
(III) f(x)gián đoạn tại x = -2
A. Chỉ (I) và (III).
B. Chỉ (I) và (II).
C. Chỉ (I).
D. Chỉ (II).
Tìm a,b để hàm số f ( x ) = x 2 + 1 k h i x ≥ 0 2 x 2 + a x + b k h i x < 0 có đạo hàm tại x = 0?
A. a = 10; b = 11
B. a = 0; b = -1
C. a = 0; b = 1
D. a = 20; b = 1
Tìm a,b để hàm số f ( x ) = x 2 + 1 k h i x ≥ 0 2 x 2 + a x + b k h i x < 0 có đạo hàm tại x = 0?
A. a = 10, b = 11
B. a = 0, b = -1
C. a = 0, b = 1
D. a = 20, b = 1
Cho hàm số f ( x ) = x + 1 + x - 1 3 x k h i x k h á c 0 2 k h i x = 0 Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 0
B. Hàm số liên tục tại mọi điểm như gián đoạn tại x = 0
C. Hàm số không liên tục tại x = 0
D. Tất cả đều sai
Giả sử hai hàm số y = f(x) và y = f(x + 0,5) đều liên tục trên đoạn [0; 1] và f(0) = f(1). Chứng minh rằng phương trình f(x) − f(x + 0,5) = 0 luôn có nghiệm trong đoạn [0; 0,5]