Chọn đáp án C
Ta có lim x → - ∞ y = 0 ; lim x → + ∞ y = 1
⇒ y = 0 ; y = 1 là các tiệm cận ngang và
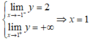
là tiệm cận đứng. Vậy đồ thị hàm số đã cho có 3 tiệm cận
Chọn đáp án C
Ta có lim x → - ∞ y = 0 ; lim x → + ∞ y = 1
⇒ y = 0 ; y = 1 là các tiệm cận ngang và
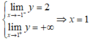
là tiệm cận đứng. Vậy đồ thị hàm số đã cho có 3 tiệm cận
Cho hàm số y = f(x) có bảng biến thiên như sau
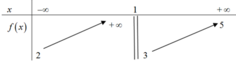
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4.
B. 1.
C. 3.
D. 2.
Cho hàm số y = f (x) có bảng biến thiên như sau
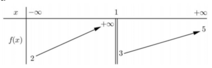
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4
B. 1
C. 3
D. 2
Cho hàm số y=f(x) có bảng biến thiên như sau:
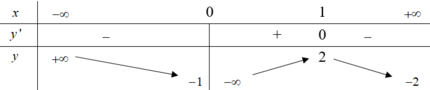
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
A. 3
B. 4
C. 1
D. 2
Cho hàm số y = f ( x ) có bảng biến thiên như hình dưới đây.
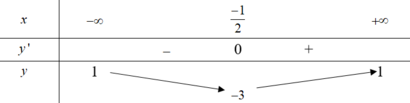
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = 1 2 f x - 1 là
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f(x) có bảng biến thiên sau:
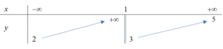
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4.
B. 1.
C. 3.
D. 2.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
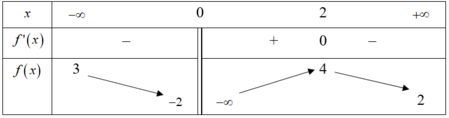
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 3
B. 4
C. 2
D. 1
Cho hàm số y=f(x) có bảng biến thiên như sau
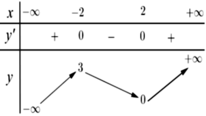
Đồ thị hàm số y= 1 f ( 3 - x ) - 2 có bao nhiêu đường tiệm cận đứng
A. 1
B. 0
C. 2
D. 3
Hàm số y = f(x) có bảng biến thiên dưới đây
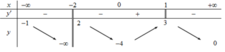
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = f(x) là
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây
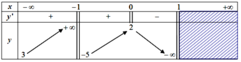
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 1.
B. 2.
C. 0.
D. 3.
Hàm số y = f(x) có đạo hàm trên R \ { -2; 2}, có bảng biến thiên như sau:
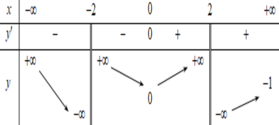
Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f ( x ) - 2018 . Tính k + l
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.