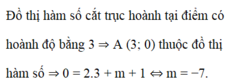Các câu hỏi tương tự
Cho hàm số y = 2x + m + 1. Tìm giá trị thực của tham số m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
A. m = 7.
B. m = 3.
C. m = -7.
D. ![]()
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
cho hàm số y=\(\sqrt{2x^2-2x-m}-x-1\)
có đồ thị (C)
tìm tất cả các giá trị nguyên dương của m để đồ thị (C) cắt trục hoành tại 2 điểm phân biệt
Cho hàm số y = 2x + m + 1. Tìm giá trị thực của m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 2
A. m = -3
B. m = 3
C. m = 0
D. m = -1
Cho hàm số y = 2(m−1)x – m 2 – 3 (d). Tìm tất cả các giá trị của m để (d) cắt trục hoành tại một điểm có hoành độ x 0 thỏa mãn x 0 < 2.
A. m < -1
B. m > 2
C. m > 1
D. m < 1
Cho hàm số y = 2x + m + 1. Tím giá trị thực của tham số m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2.
A. m = -3.
B. m = 3.
C. m = 0.
D. m = -1.
Cho hàm số bậc nhất y ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5. A.
a
1
6
;
b
5
6
B.
a
−
1
6
;
b
−
5
6
C.
a
1
6...
Đọc tiếp
Cho hàm số bậc nhất y = ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5.
A. a = 1 6 ; b = 5 6
B. a = − 1 6 ; b = − 5 6
C. a = 1 6 ; b = − 5 6
D. a = − 1 6 ; b = 5 6
Cho hàm số y = \(\frac{x^2-mx+m}{x-m}\). Hãy xác định m sao cho:
a) Đồ thị của hàm số không cắt trục tung
b) Đồ thị của hàm số không cắt trục hoành
c) Đồ thị của hàm số cắt trục hoành tại 2 điểm phân biệt
cho hàm số y=x2 - mx - m - 1 (m ϵ R) . Gọi S là tập hợp tất cả các giá trị của m để đồ thị đã cho cắt trục hoành tại 2 điểm phân biệt có hoành độ x1 ; x2 thỏa mãn |x1|+|x2|=4 . Tổng tất cả các phần tử của S là bao nhiêu