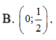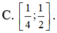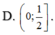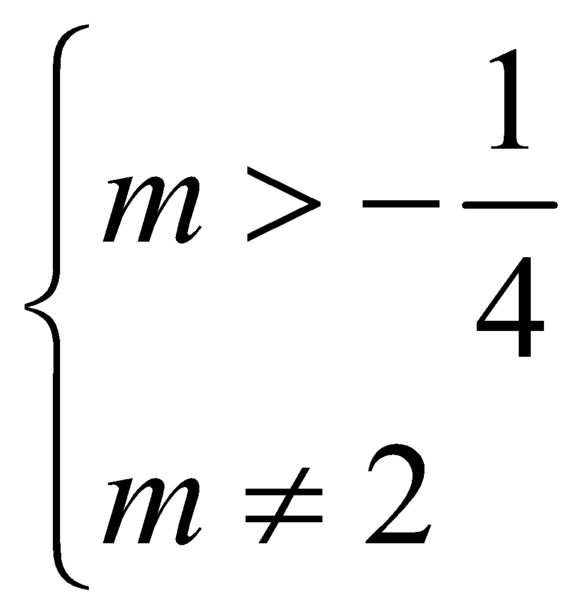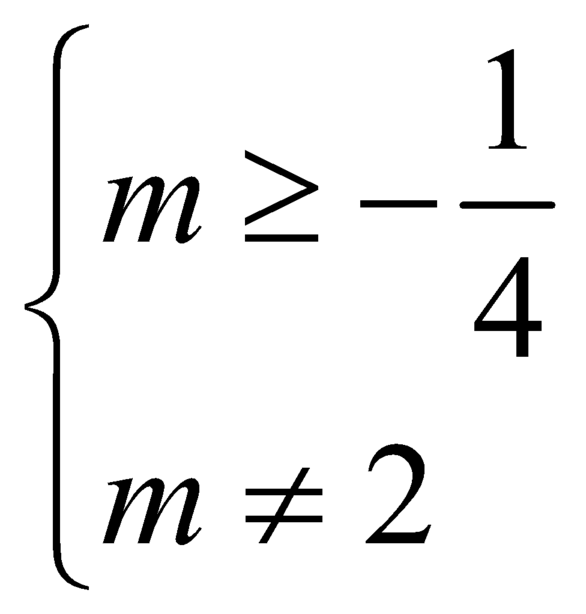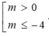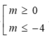ĐKXĐ: 0 ≤ x ≤ 4 x 2 - 6 x + 2 m > 0
Ta có
12
+
4
x
-
x
2
≠
0
∀
x
nên để ( C) có hai tiệm cận đứng thì phương trình
x
2
-
6
x
+
2
m
=
0
⇔
x
2
-
6
x
+
2
m
=
0
(
*
)
có hai nghiệm phân biệt thuộc [ 0; 4]
Đế phương trình có 2 nghiệm phân biệt thì ∆ ' = 9 - 2 m > 0 ⇔ m < 9 2
Gọi 2 nghiệm phân biệt của (*) là x1< x2 ta có 0≤ x1< x2≤ 4.
Theo định lí Vi-et ta có x 1 + x 2 = 6 x 1 x 2 = 2 m
Khi đó

Kết hợp nghiệm ta có 4 ≤ m ≤ 9 2
Mà m nguyên nên m= 4
Chọn B.