Đáp án B
Gọi A là điểm thuộc đồ thị hàm số có hoành độ bằng 2, khi đó A(2;1)
Vì  nên
nên ![]() .
.
Phương trình tiếp tuyến cần tìm là
![]()
![]() .
.
Đáp án B
Gọi A là điểm thuộc đồ thị hàm số có hoành độ bằng 2, khi đó A(2;1)
Vì  nên
nên ![]() .
.
Phương trình tiếp tuyến cần tìm là
![]()
![]() .
.
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho hàm số y = 2 x có đồ thị (C) và đường thẳng d là tiếp tuyến của (C ) tại điểm có hoành độ bằng 2. Hệ số góc của đường thẳng d là
A. ln 2
B. 2ln 2
C. 4 ln 2
D. 4ln 3
Cho hàm số ![]() có đồ thị
có đồ thị ![]() . Phương trình tiếp tuyến của đồ thị
. Phương trình tiếp tuyến của đồ thị ![]() tại tiếp điểm có hoành độ bằng 1 là:
tại tiếp điểm có hoành độ bằng 1 là:
A. ![]() .
.
B. ![]() .
.
C.![]() .
.
D. ![]() .
.
Cho hàm số y = x3 + ax2 + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:
A. k = 0
B. k = 24
C. k = -18
D. k = 18
Cho hàm số y= x4- 2mx2+m (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( ¾; 1) đến đường thẳng d đạt giá trị lớn nhất?
A. 0
B. 1
C. 2
D. 3
Cho hàm số y=(x+1)/(2x-1) Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ bằng – 1 có hệ số góc bằng
A.![]()
B. ![]()
C. ![]()
D. –![]()
Cho hàm số y = x 3 + a x 2 + b x + c có đồ thị (C) . Biết rằng tiếp tuyến d của (C) tại điểm A có hoành độ bằng -1 cắt (C) tại B có hoành độ bằng 2 (xem hình vẽ). Diện tích hình phẳng giới hạn bởi d và (C) (phần gạch chéo trong hình vẽ) bằng:
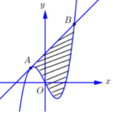
A. 27 4
B. 11 2
C. 25 4
D. 13 2
Cho hàm số ![]() có đồ thị
có đồ thị ![]() . Gọi
. Gọi ![]() là tiếp tuyến của
là tiếp tuyến của ![]() tại điểm
tại điểm ![]() có hoành độ
có hoành độ ![]() Biết
Biết ![]() cắt
cắt ![]() tại hai điểm phân biệt
tại hai điểm phân biệt ![]()
![]() có hoành độ lần lượt là
có hoành độ lần lượt là ![]() Cho biết
Cho biết 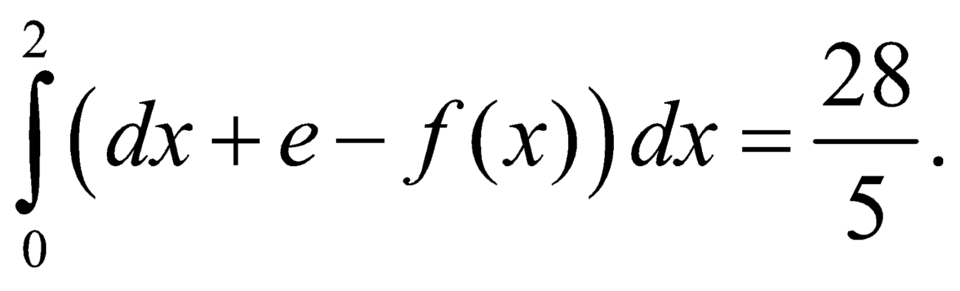 Tích phân
Tích phân 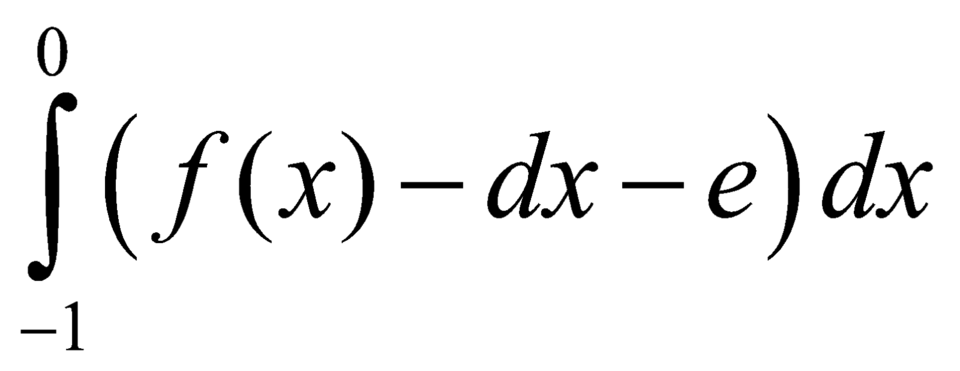 bằng:
bằng:
A. 2/5
B. 1/4
C. 2/9
D. 1/5
Phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm có hoành độ bằng 1 là:
tại điểm có hoành độ bằng 1 là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.