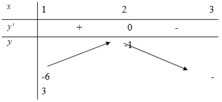
Phương trình tương đương với:
m = g ( x ) = x 2 - 6 x + 12 f ( x - 1 ) .
Ta có
g ' ( x ) = 2 x - 6 f ( x - 1 ) + x 2 - 6 x + 12 f ' ( x - 1 )
+) Nếu 2 ≤ x < 3
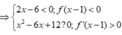
⇒ g ' ( x ) > 0
+) Nếu x=3
![]()
+) Nếu 3 < x ≤ 4
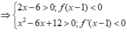
⇒ g ' ( x ) < 0 .
Vậy trên đoạn [2;4] ta có g'(x)=0 ↔ x=3.
Bảng biến thiên:
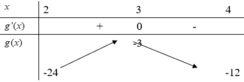
Vậy phương trình có hai nghiệm phân biệt trên đoạn
2 ; 4 ⇔ - 12 < m < 3 ⇒ m ∈ - 12 , . . . , - 4 .
Tổng các số nguyên cần tìm bằng ∑ k = - 12 - 4 k = - 72
Chọn đáp án B.