Đáp án A.
Phương pháp: Hàm số y = f(x) liên tục tại ![]()
Cách giải: 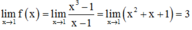
f(1) = 2m+1
Để hàm số liên tục tại x = 1
![]()
Đáp án A.
Phương pháp: Hàm số y = f(x) liên tục tại ![]()
Cách giải: 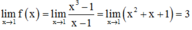
f(1) = 2m+1
Để hàm số liên tục tại x = 1
![]()
Cho hàm số y=f(x) có đạo hàm liên tục trên − 1 ; 2 . Đồ thị của hàm số y=f'(x) được cho như hình vẽ. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f − 1 = 19 12 , tính f(2).
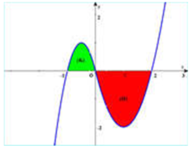
A. f 2 = 23 6 .
B. f 2 = − 2 3 .
C. f 2 = 2 3 .
D. f 2 = 11 6 .
Cho hàm số y =f(x) có đạo hàm liên tục trên [-1;2]. Đồ thị của hàm số y = f'(x) được cho như hình bên. Diện tích các hình phẳng (K), (H) lần lượt là 5 12 và 8 3 . Biết f - 1 = 19 12 , tính f(2)
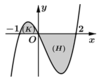
A. f 2 = - 2 3
B. f 2 = 2 3
C. f 2 = 11 6
D. f 2 = 3
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020
Cho hàm số f ( x ) = x 3 + m x 2 + x + 1 Gọi k là hệ số góc tiếp tuyến của đồ thị hàm số tại M có hoành độ x = 1. Tất cả các giá trị thực của tham số m để thỏa mãn k.f(-1)<0
![]()
![]()
![]()
![]()
Cho hàm số f x = x 4 - 4 x 2 + 6 x + 1 Hệ số góc k của tiếp tuyến của đồ thị hàm số f’(x) tại điểm có hoành độ x = 1 là
A. k = -4
B. k = -8
C. k = 4
D. k = 20
Cho hàm số f(x) thỏa mãn f ' x 2 + f x . f " x = 2018 x ∀ x ∈ R và f(0) = f’(0) = 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2
B. V = 4036π
C. V = 8090 3 π
D. V = 8090π/3
Cho hàm số f(x) có đạo hàm f ’ ( x ) = x 2019 ( x - 1 ) 2 ( x + 1 ) 3 . Số điểm cực đại của hàm số f(x) là
A. 1
B. -1
C. 0
D. 3
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Cho hàm số f(x) thỏa mãn f ' x 2 + f x f ' ' x = 2018 x , ∀ x ∈ ℝ và f 0 = f ' 0 = 1 . Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0 , x = 2 . Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2 π
B. V = 4036 π
C. V = 8090 3 π
D. V = 8090 3 π
Cho hàm số f(x) có đạo hàm f'(x) = ( x + 1 ) 2 ( x - 1 ) 3 ( 2 - x ) . Hỏi hàm số đồng biến trên khoảng nào dưới đây?
A. (1;2)
B. (-1;1)
C. ( - ∞ ; 1 )
D. ( 2 ; + ∞ )