Đặt t=f(x)+1 phương trình trở thành
![]()
![]()
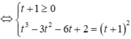

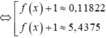
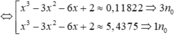
Chọn đáp án A.
Đặt t=f(x)+1 phương trình trở thành
![]()
![]()
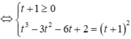

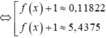
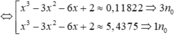
Chọn đáp án A.
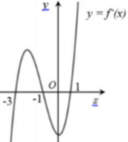
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
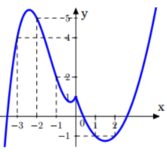
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Cho hàm số y = f (x) có bảng biến thiên như sau
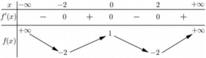
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
Cho hàm số f ( x ) = x 4 - 4 x 2 + 1 Khi đó, phương trình f ( f ( f ( x ) - 1 ) - 2 ) = 1 có bao nhiêu nghiệm thực phân biệt
A. 24
B. 22
C. 26
D. 32
Cho hàm số f ( x ) = 1 3 x 3 - x 2 + x + 3 - log 3 m Có bao nhiêu số nguyên m để phương trình f ( f ( f ( f ( x ) ) ) ) = x có 3 nghiệm thực phân biệt
A. 20
B. 18
C. 19
D. 17
Cho hàm số f ( x ) = a x 2 + 2 b x 3 - 3 c x 2 - 4 d x + 5 h (a,b,c,d,hÎZ). Hàm số y=f’(x) có đồ thị như hình vẽ bên. Tập nghiệm thực của phương trình f(x)=5h có số phần tử bằng
A. 3
B. 4
C. 2
D. 1
Cho hàm số y=f(x) thoả mãn f(-2)=3, f(2)=2 và bảng xét dấu của đạo hàm như sau:
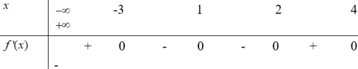
Bất phương trình 3 f ( x ) + m ≤ 4 f ( x ) + 1 + 4 m nghiệm đúng với mọi số thực x ∈ - 2 ; 2 khi và chỉ khi
A. m ∈ - 2 ; - 1
B. m ∈ - 2 ; - 1
C. m ∈ - 2 ; 3
D. m ∈ - 2 ; 3
Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn f(x)>0,∀x∈R. Biết f(0)=1 và (2-x)f(x)-f' (x)=0. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)=m có hai nghiệm phân biệt.
A. m< e 2 .
B. 0<m< e 2 .
C. 0<m≤ e 2 .
D. m > e 2
Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để phương trình f(f(x+1))=m có ít nhất 6 nghiệm thực phân biệt ?
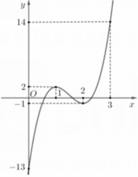
A. 2.
B. 3.
C. 5.
D. 4.
Cho hàm số f(x) có đạo hàm liên tục trên và thỏa mãn f ( x ) > 0 , ∀ ∈ ℝ . Biết f(0) = 1 và f ' x f x = 2 - 2 x . Tìm các giá trị thực của tham số m để phương trình f(x) = m có hai nghiệm thực phân biệt.
A. m > e
B. 0 < m ≤ 1
C. 0 < m < e
D. 1 < m < e