Đáp án là B.
• Trường hợp m = 0
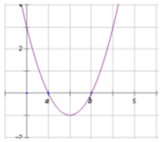
f x = − x 2 + 1 có đồ thị là parabol, có đỉnh I(0;-1).
Đồ thị hàm số đã cho có một điểm cực đại là I thuộc trục tung.
Do đó m = 0 thoả yêu cầu bài toán.
• Trường hợp m ≠ 0
f ' x = 4 m x 3 − 2 m + 1 x
f ' x = 0 ⇔ x = 0 ∨ x 2 = m + 1 2 m
+ Nếu − 1 ≤ m < 0 thì f ' ( x ) = 0 có nghiệm x = 0 ( y = m + 1 )

Đồ thị hàm số có một điểm cực đại (0;m+1) thuộc trục toạ độ.
+ Nếu m < − 1 ∨ m > 0 thì f ' ( x ) = 0 có ba nghiệm phân biệt
x = 0 y = m + 1 x = m + 1 2 m ( y = 3 m 2 + 2 m − 1 4 m ) x = − m + 1 2 m ( y = 3 m 2 + 2 m − 1 4 m )
Khi đó đồ thị hàm số có các điểm cực trị thuộc các trục toạ độ khi và chỉ khi 3 m 2 + 2 m − 1 = 0 ⇔ m = − 1 ∨ m = 1 3 . Nhận m = 1 3