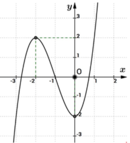
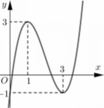
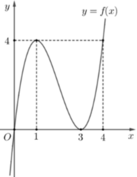
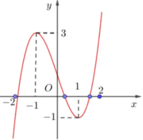
Chọn đáp án D
Đặt t = sinx với x∈[0;π] thì t∈[0;1] và phương trình trở thành: f(t)=m (1).
Với t=1 phương trình có nghiệm duy nhất x = π 2 ∈ 0 ; π
với mỗi t∈[0;1) phương trình có hai nghiệm thuộc đoạn [0;π] là arcsint;π−arcsint
Vậy phương trình đã cho có đúng hai nghiệm thuộc đoạn [0;π]
⇔(1) có đúng một nghiệm thuộc nửa khoảng [0;1).[0;1).
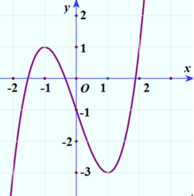
Quan sát đồ thị hàm số ta - 1 < m ≤ 1 ⇒ m ∈ 0 ; 1