Đáp án C.
Ghi nhớ: Công thức đường trung tuyến:
m a 2 = b 2 + c 2 2 − a 2 4 .
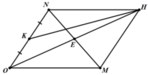
Gọi E là giao điểm của OH và MN.
Ta có:
O E 2 = O M 2 + O N 2 2 − M N 2 4 = 17 − 9 2 = 25 2 ⇒ O H 2 = 50.
H K 2 = H N 2 + H O 2 2 − O N 2 4 = O M 2 + O H 2 2 − O N 2 4 = 17 + 50 2 − 17 4 = 117 4 ⇒ H K = 3 13 2 .