Các câu hỏi tương tự
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu
V
1
,
V
2
lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số
V
1
V
2...
Đọc tiếp
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu V 1 , V 2 lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số V 1 V 2 là
![]()
![]()
![]()
![]()
Cho khối nón có độ lớn góc ở đỉnh là
π
3
. Một khối cầu
(
S
1
)
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3...
Đọc tiếp
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 1 ;..; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , . . . . . , V n - 1 , V n , lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , . . . . . , S n - 1 , S n , và V là thể tích của khối nón. Tính giá trị của biểu thức T = l i m V 1 + V 2 + . . . + V n V .
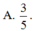
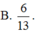
![]()
![]()
Một khối đồ chơi gồm một khối nón (N) xếp chồng lên một khối trụ (T). Khối trụ (T) có bán kính đáy và chiều cao lần lượt là
r
1
,
h
1
. Khối nón (N) có bán kính đáy và chiều cao lần lượt là
r
2
,
h
2
thỏa mãn
r
2
2
3
r...
Đọc tiếp
Một khối đồ chơi gồm một khối nón (N) xếp chồng lên một khối trụ (T). Khối trụ (T) có bán kính đáy và chiều cao lần lượt là r 1 , h 1 . Khối nón (N) có bán kính đáy và chiều cao lần lượt là r 2 , h 2 thỏa mãn r 2 = 2 3 r 1 và h 1 = h 2 . Biết rằng thể tích toàn bộ khối đồ chơi bằng 124 c m 3 . Thể tích khối nón (N) bằng:
![]()
![]()
![]()
![]()
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N).
S
x
q
,
S
t
p
,
V
lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai A.
V
1
3
π
r
h
B. ...
Đọc tiếp
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). S x q , S t p , V lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A. V = 1 3 π r h
B. l 2 = h 2 + r 2
C. S t p = π r 1 + r
D. S x q = π r l
Một khối trụ tròn có 1 đường tròn đáy thuộc mặt bên của 1 hình nón xoay, đáy còn lại thuộc mặt đáy hình nón. Biết chiều cao hình trụ bằng nửa chiều cao hình nón. Tính tỷ số
k
V
1
V
2
với
V
1
,
V
2
tương ứng là thể tích hình trụ và hình nón.
Đọc tiếp
Một khối trụ tròn có 1 đường tròn đáy thuộc mặt bên của 1 hình nón xoay, đáy còn lại thuộc mặt đáy hình nón. Biết chiều cao hình trụ bằng nửa chiều cao hình nón. Tính tỷ số k = V 1 V 2 với V 1 , V 2 tương ứng là thể tích hình trụ và hình nón.
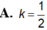
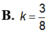
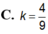
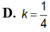
Một hình nón có chiều cao 9(cm) nội tiếp trong một hình cầu có bán kính 5(cm) . Gọi
V
1
,
V
2
lần lượt là thể tích của khối nón và khối cầu. Tính tỉ số
V
1
V
2
.
Đọc tiếp
Một hình nón có chiều cao 9(cm) nội tiếp trong một hình cầu có bán kính 5(cm) . Gọi V 1 , V 2 lần lượt là thể tích của khối nón và khối cầu. Tính tỉ số V 1 V 2 .
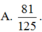
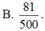
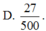
Một cái “cù” (đồ chơi trẻ em) gồm hai khối: khối trụ
H
1
và khối nón
H
2
như hình bên. Chiều cao và bán kính khối trụ lần lượt bằng
h
1
,
r
1
, chiều cao và bán kính đáy của khối nón lần lượt bằng
h
2
,
r
2
thỏa mãn
h...
Đọc tiếp
Một cái “cù” (đồ chơi trẻ em) gồm hai khối: khối trụ H 1 và khối nón H 2 như hình bên. Chiều cao và bán kính khối trụ lần lượt bằng h 1 , r 1 , chiều cao và bán kính đáy của khối nón lần lượt bằng h 2 , r 2 thỏa mãn h 1 = 1 3 h 2 , r 1 = 1 2 r 2 . Biết thể tích toàn khối là 30cm, thể tích khối H 1 bằng
![]()
![]()

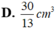
Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao của hình nón. Giả sử khoảng cách từ trung điểm của IO tới một đường sinh bất kì là
2
. Hai điểm A, B nằm trên đường tròn tâm O sao cho AB 1/2. Tính thể tích khối tứ diện IABO A.
63
12
B.
7
6
C.
255
12...
Đọc tiếp
Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao của hình nón. Giả sử khoảng cách từ trung điểm của IO tới một đường sinh bất kì là 2 . Hai điểm A, B nằm trên đường tròn tâm O sao cho AB = 1/2. Tính thể tích khối tứ diện IABO
A. 63 12
B. 7 6
C. 255 12
D. 5 4
Một khối đồ chơi gồm một khối hình trụ (T) gắn chồng lên một khối hình nón (N), lần lượt có bán kính đáy và chiều cao tương ứng là
r
1
,
h
1
,
r
2
,
h
2
thỏa mãn
r
2
2
r
1
;
h
1
2...
Đọc tiếp
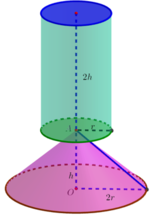
Một khối đồ chơi gồm một khối hình trụ (T) gắn chồng lên một khối hình nón (N), lần lượt có bán kính đáy và chiều cao tương ứng là r 1 , h 1 , r 2 , h 2 thỏa mãn r 2 = 2 r 1 ; h 1 = 2 h 2 (hình vẽ). Biết rằng thể tích của khối nón (N) bằng 20 c m 3 . Thể tích của toàn bộ khối đồ chơi bằng
![]()
![]()
![]()
![]()

