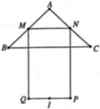
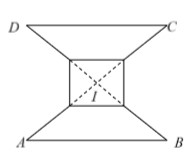
Cho hai hình vuông có cạnh đều bằng 5 được xếp lên nhau sao cho đỉnh M của hình vuông này là tâm của hình vuông kia, đường chéo MN vuông góc với cạnh PQ tạo thành hình phẳng (H) ( như hình vẽ bên).
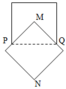
Tính thể tích V của vật thể tròn xoay khi quanh hình (H) quanh trục MN.
A. V = 125 ( 1 + 2 ) π 6
B. V = 125 ( 5 + 2 2 ) π 12
C. V = 125 ( 5 + 4 2 ) π 24
D. V = 125 ( 2 + 2 ) π 4
Đáp án A.
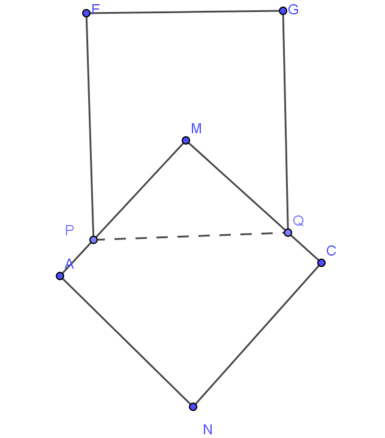
Gọi V 1 là thể tích khối trong xoay khi xoay hình vuông EGQP quanh MN. Khối này có bán kính đáy R = 1 2 E G = 5 2 và đường cao = EP = 5 => V 1 = 5 . 5 2 2 π = 125 4 π
Gọi V 2 là thể tích khối tròn xoay khi xoay hình vuông AMCN quanh MN, khối này là hợp lại của 2 khối nón đêu có bán kính đáy R = 1 2 A C = 5 2 2 Đường cao h = 1 2 M N = 5 2 2 => V 2 = 2 . 1 3 . 5 2 2 . 5 2 2 2 π = 125 2 6 π
Gọi V 3 là thể tích của khối nón tròn xoay khi quay MPQ quanh MN, khối này óc bán kính đáy R = 1 2 P Q = 5 2 đường cao h = d ( M ; P Q ) = 5 2 => V 3 = 1 3 . 5 2 . 5 2 2 . π = 125 12 π
Ta có thể tích của toàn khối tròn xoay V = V 1 + V 2 - V 3 = 125 1 + 2 π 6