tham khảo
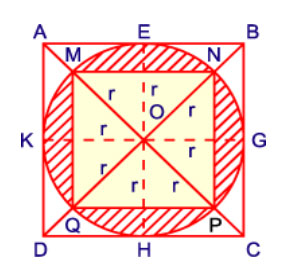
Diện tích tam giác ABD là:
(12 x (12 : 2))/2 = 36 (cm2)
Diện tích hình vuông ABCD là:
36 x 2 = 72 (cm2)
Diện tích hình vuông AEOK là:
72 : 4 = 18 (cm2)
Do đó: OE x OK = 18 (cm2)
r x r = 18 (cm2)
Diện tích hình tròn tâm O là:
18 x 3,14 = 56,92 (cm2)
Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2)
Diện tích hình vuông MNPQ là:
9 x 4 = 36 (cm2)
Vậy diện tích phần gạch chéo là:
56,52 - 36 = 20,52 (cm2)
refer
Diện tích tam giác ABD là:
(12 x (12 : 2))/2 = 36 (cm2)
Diện tích hình vuông ABCD là:
36 x 2 = 72 (cm2)
Diện tích hình vuông AEOK là:
72 : 4 = 18 (cm2)
Do đó: OE x OK = 18 (cm2)
r x r = 18 (cm2)
Diện tích hình tròn tâm O là:
18 x 3,14 = 56,92 (cm2)
Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2)
Diện tích hình vuông MNPQ là:
9 x 4 = 36 (cm2)
Vậy diện tích phần gạch chéo là:
56,52 - 36 = 20,52 (cm2)