Cho hai hình bình hành ABCD và ABEF có tâm lần lượt là O, O’ và không cùng nằm trong một mặt phẳng. gọi M là trung điểm của AB.
(I) (ADF) // (BCE) (II) (MOO’) // (ADF)
(III) (MOO’) // (BCE) (IV) (AEC) // (BDF)
Khẳng định nào sau đây là đúng
A.chỉ có (1) đúng
B. chỉ có (1) và (2) đúng
C. (I), (II), (III) đúng
D. chỉ có (1) và (IV) đúng
Đáp án C
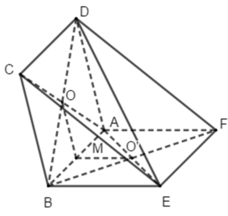
+) Ta có: BC // AD; BE // AF (ABCD và ABEF là hình bình hành)
Suy ra BC // (ADF); BE // (ADF)
Mà BC ∩ BE = B
Do đó (ADF) // (BEC).
+) O và O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O và O’ là trung điểm của BF và BD
Xét tam giác ABF có MO’ là đường trung bình nên MO’ // AF
MO’ // (ADF) (1)
Tương tự MO là đường trung bình của tam giác ABD nên MO // AD
MO // (ADF) (2)
Từ (1) và (2) suy ra (MOO’) // (ADF)
+) Chứng minh tương tự ta cũng có (MOO’) // (BCE).
+) Hai mặt phẳng (AEC) và (BDF) có:
AC ∩ DB = O ; AE ∩ BF = O’
Suy ra (AEC) ∩ (BDF) = OO’.
Vậy khẳng định (I); (II); (III) đúng.