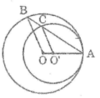
Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
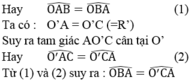
Suy ra: OB // O’C (vì có hai góc ở vị trí đồng vị bằng nhau)

Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
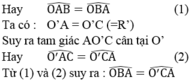
Suy ra: OB // O’C (vì có hai góc ở vị trí đồng vị bằng nhau)
Cho đường tròn (O ; 3cm) và đường tròn (O’; 1cm) tiếp xúc ngoài tại A. Vẽ hai bán kính OB và O’C song song với nhau thuộc cùng nửa mặt phẳng có bờ OO’. Tính số đo góc BAC.
Cho hình bên, trong đó hai đường tròn (O) và (O’) tiếp xúc với nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau.
Cho (O,9cm) và (O’,3cm) tiếp xúc tại A. Vẽ 2 bán kính OB và O’C song song với nhau và thuộc cùng 1 mặt phẳng bờ OO’ a) tính số đo gics BAC b) gọi I là giao của BC và OO’ . Tính OI Mình dg cần gấp lắm ạ
Cho đường tròn (O') tiếp xúc với hai cạnh Ox và Oy của xOy tại A và B. Từ A kẻ tia song song với OB cắt (O') tại C. Đoạn oc cắt (O') tại E. Hai đường thẳng AE và OB cắt nhau tại K. Chứng minh K là trung điểm của OB
Cho các đường tròn (O; R) và (O’; R’) tiếp xúc trong với nhau tại A (R > R’). Vẽ đường kính AB của (O), AB cắt (O’) tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O’), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:
a, AP là phân giác của B A Q ^
b, CP và BR song song với nhau
Cho đường tròn (O) và đường tròn (O') tiếp xúc ngoài với nhau tai A. Trên đường tròn (O) lấy điểm B sao cho ba điểm A, O, B không thẳng hàng. Đường thẳng AB cắt đưởng tròn (O') tại điểm thứ hai là C (C khác A). Chứng minh OB song song với O'C.
Cho đường tròn O bán kính R và hai điểm A, B nằm trên đường tròn (AB không là đường kính). Các tiếp tuyến tại A, B của đường tròn cắt nhau tại M. Kẻ cát tuyến MCD với đường tròn (C nằm giữa M và D)
a, Chứng minh các tam giác MBC và MDB đồng dạng
b, Chứng minh tứ giác MAOB là nội tiếp
c, Khi AB = R 3 , tính bán kinh đường tròn ngoại tiếp tứ giác MAOB theo R
d, Kẻ dây AE của (O) song song với MD. Nối BE cắt MD tại I. Chứng minh I là trung điểm của CD
1. Cho các đường tròn (O;R) và (O';R') tiếp xúc trong với nhau tại A(R>R'). Vẽ đường kính AB của (O) , AB cắt (O') tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O'), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:
a) AP là phân giác của góc BAQ
b) CP và BR song song với nhau
2. Cho đường tròn (O;R) vơi SA là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyến thứ hai MB với đường tròn (O). gọi I là trung điểm MA, K là giao điểm của BI với (O)
a) Chứng minh các tam giác IKA và IAB đồng dạng. Từ đó suy ra tam giác IKM đồng dạng với tam giác IMB
b) Giả sử MK cắt (O) tại C. Chứng minh BC song song MA
3. Cho tam giác ABC nội tiếp đường tròn (O) và AB<AC. Đường tròn (I) đi qua B và C, tiếp xúc với AB tại B cắt đường thẳng AC tại D. Chứng minh OA và BD vuông góc với nhau.
4.Cho hai đường tròn (O) và (I) cắt nhau tại C và D, trong đó tiếp tuyến chung MN song song với cát tuyến EDF, M và E thuộc (O), N và F thuộc (I), D nằm giữa E và F. Gọi K ,H theo thứ tự là giao điểm của NC,MC và EF. Gọi G là giao điểm của EM ,FN. Chứng minh:
a) Các tam giác GMN và DMN bằng nhau
b) GD là đường trung trực của KH
Làm ơn giúp mình với !!! Chút nữa là mình đi học rồi !!!! Cảm ơn trước !!!