Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tam giác AIO vuông tại A có AM ⊥ IO
Theo hệ thức lượng trong tam giác vuông, ta có: I A 2 = IM.IO (1)
Tam giác AIO’ vuông tại A có AN ⊥ IO’
Theo hệ thức lượng trong tam giác vuông, ta có: I A 2 = IN.IO’ (2)
Từ (1) và (2) suy ra: IM.IO = IN.IO’
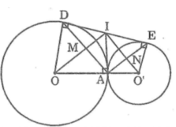
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. Tứ giác AMIN là hình gì? Vì sao?
Cho 2 đường tròn O và O' tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE (D thuộc đường tròn (O), E thuộc đường tròn (O')). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O'I và AE
a) Tứ giác AMIN là hình gì?
b) Chứng minh IM.IO = IN.IO'
c) Chứng minh OO' là tiếp tuyến của đường tròn đường kính DE
d) Tính DE biết OA = 5cm và O'A = 3,2cm
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. Tính độ dài DE, biết rằng OA = 5cm, O’A = 3,2cm
Cho (o) và (o') tiếp xúc ngoài tại A,kẻ tiếp tuyến chung ngoài DE ,D thuộc (o),E thuộc (o').kẻ tiếp tuyến chung trong tại A,cắt DE ở I.Gọi OI giao AD tại M,O'I giao AE tại N
a,CM AMIN là hình gì? tại sao?
b,CM IM .IO=IN.IO'
c,OO' là tiếp tuyến của đường tròn đường kính DE
d,tính DE biết OA=5cm,O'A =3,2cm
Bài 3. (4 điểm) Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B ∈ (O); C ∈ (O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC tại I. a) Chứng minh rằng góc BAC = 900 b) Trên tia đối của tia IA lấy điểm D sao cho IA = ID. Tứ giác ABDC là hình gì? Vì sao? c) Tính độ dài BC trong trường hợp OA = 7,2cm và O’A = 3,2cm d) Gọi giao điểm của OI và AB là M; giao điểm của O’I và AC là N.
Cho hai đường tròn (O,R)và (O`,r) tiếp xúc ngoài tại A kẻ tiếp tuyến chung ngoài DE của (O)và (O`), D€(O),E€(O')tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài DE ở I
a,tính số đo góc OIO'.
b, chứng minh OO' là tiếp tuyến của đường tròn đường kính DE
c, tính độ dài DE theo R và r
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn (D ∈ (O), E ∈ (O’)). Gọi M là giao điểm của BD và CE. Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn.
cho hai tiếp tuyến đường tròn tâm (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B thuộc (O), (C) thuộc (O'). tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoaig BC tại I. a, Cminh góc BAC =90 độ. b,trên tia đối của tía IA lấy điểm D sao cho IA=ID. Tứ giác ABDC là hình gì, vì sao. c, gọi giao điểm của OI và AB là M; giao điểm của O'I và AC là N, chứng minh rằng OM/O'N=OI^3/O'I^3
