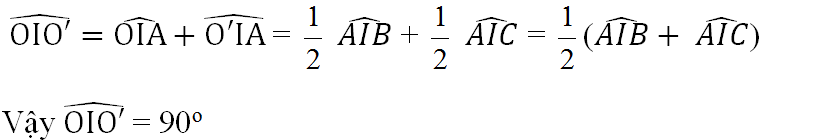a) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
\(\Delta ABC\) có đường trung tuyến\(AI=\frac{1}{2}BC\) nên \(\Delta ABC\) vuông tại A
\(\Rightarrow\widehat{BAC}=90^o\left(dpcm\right)\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
\(IA^2\) = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
Cho hai đường tròn (O), (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B∈(O);C∈(O′)B∈(O);C∈(O′). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I
a) Chứng minh rằng ˆBAC=900BAC^=900
b) Tính số đo góc OIO'
c) Tính độ dài BC, biết OA = 9cm, O'A = 4cm
Cho hai đường tròn (O), (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, \(B\in\left(O\right);C\in\left(O'\right)\). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I
a) Chứng minh rằng \(\widehat{BAC}=90^0\)
b) Tính số đo góc OIO'
c) Tính độ dài BC, biết OA = 9cm, O'A = 4cm
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O'). Gọi P là điểm đối xứng với M qua OO', Q là điểm đối xứng với N qua OO'. Chứng minh rằng :
a) MNQP là hình thang cân
b) PQ là tiếp tuyến chung cả hai đường tròn (O) và (O')
c) MN + PQ = MP + NQ
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO'C. Gọi DE là tiếp tuyến chung của hai đường tròn. \(D\in\left(O\right),E\in\left(O'\right)\). Gọi M là giao điểm của BD và CE
a) Tính số đo góc DAE
b) Tứ giác ADME là hình gì ? Vì sao ?
c) Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn \(\left(C\in\left(O\right),D\in\left(O'\right)\right)\)
a) Tính số đo góc CAD
b) Tính độ dài CD biết OA = 4,5, O'A = 2cm
1) Cho (I;2cm) (O) đường kính 8cm tiếp xúp tại C, AB là tiếp tuyến của hai đường tròn. Tính tứ giác ABOI
2) Cho (O;3cm)(I;1cm) tiếp xúp tại C tiếp tuyến chung AB của hai đường tròn cắt OI tại M. Tính MC
3) Cho (O;12cm)(O'16cm) chát nhau tại A và B sao cho OA là tiếp tuyến của đường tròn (O'). Tính dây AB
1/ Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ tiếp tuyến chung MAN sao cho MA = AN. Đường vuông góc với MN tại A cắt OO' tại I. Chứng minh I là trung điểm của OO'
2/ Cho hai đường tròn (o) và (o') tiếp xúc ngoài nhau tại A gọi M là giao diểm một trong hai tiếp tuyến chung ngoài BC và tiếp tuyến chung trong c/m BC là tiếp tuyến của đường tròn đường kính OO' tại M
Mọi người vẽ giúp em hình vẽ của hai bài toán này gấp với ạ!!!!!!!!!!
Cho đường tròn tâm O, vẽ tia Ox cố định và lấy A di chuyển trên tia đó.Dựng BC là tiếp tuyến chung ngoài của(O) và (A,AO) với B, C là các tiếp điểm (B∈(O), C∈(A)).Chứng minh rằng C nằm trên đường thẳng cố định khi A di chuyển.
Em cảm ơn!
Cho hai đường tròn (O; 2cm) và (O'; 3cm). OO' = 6cm
a) Hai đường tròn (O), (O') có vị trí tương đối như thế nào đối với nhau ?
b) Vẽ đường tròn (O'; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó (A là tiếp điểm). Tia O'A cắt đường tròn (O';3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O'B, B và C thuộc cùng một nửa mặt phẳng có bờ OO'. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O; 2cm) và (O'; 3cm)
c) Tính độ dài BC
d) Gọi I là giao điểm của BC và OO'. Tính độ dài IO ?