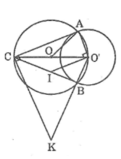
Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C
Suy ra: ![]() (tính chất hai tiếp tuyến cắt nhau)
(tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Suy ra: O’I // CA => ![]() (hai góc so le trong)
(hai góc so le trong)
Suy ra: ![]()
Hay tam giác CIO’ cân tại I => IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: ![]() (tính chất hai tiếp tuyến cắt nhau)
(tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A => ![]() (hai góc so le trong)
(hai góc so le trong)
Suy ra: ![]()
Hay tam giác CKO’ cân tại K => KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C
Vậy O, I, K thẳng hàng.

