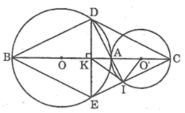
Tam giác ABD nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại D
Suy ra: AD ⊥ BD
Tứ giác BDCE là hình thoi nên EC // BD
Suy ra: EC ⊥ AD (1)
Tam giác AIC nội tiếp trong đường tròn (O’) có AC là đường kính nên vuông tại I
Suy ra: AI ⊥ CE (2)
Từ (1) và (2) suy ra AD trùng với AI
Vậy D, A, I thẳng hàng.

