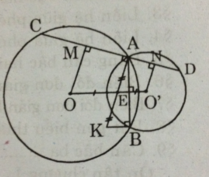
 Kẻ OM ⊥ AD.
Kẻ OM ⊥ AD.
Theo tính chất đường kính vuông góc với một dây, ta có: MA = MC
Tương tự, kẻ O'N ⊥ AD => NA = ND.
Ta có:
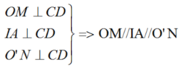
Vậy tứ giác OMNO' là hình thang vuông.
Ta còn có: IO = IO' (gt) và IA // OM
Do đó IA là đường trung bình của hình thang OMNO'.
=> AM = AN hay 2AM = 2AN
Hay AC = CD (đpcm)

