Question

Cho hai đường tròn (O; 2cm), (O’; 3cm), OO’ = 6cm. Vẽ đường tròn (O’; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó (A là tiếp điểm). Tia O’A cắt đường tròn (O’; 3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O’B, B và C thuộc cùng một nửa mặt phẳng có bờ OO’. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O; 2cm), (O’; 3cm).

Answer 1

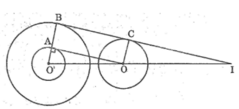
Xét tứ giác ABCO ta có:

AB // CO (gt)    (1)

Mà : AB = O’B – O’A = 3 – 1 = 2    (cm)

Suy ra: AB = OC = 2 (cm) (2)

Từ (1) và (2) suy ra: ABCO là hình bình hành

Lại có: OA ⊥ O’A (tính chất tiếp tuyến)

Suy ra: BC ⊥ OC và BC ⊥ O’B

Vậy BC là tiếp tuyến chung của hai đường tròn (O) và (O’)