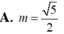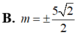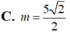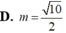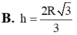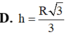Cho hai đường tròn C 1 , C 2 lần lượt chứa trong hai mặt phẳng phân biệt (P), (Q), ( C 1 ) , ( C 2 ) có hai điểm chung A, B. Hỏi có bao nhiêu mặt cầu có thể đi qua ( C 1 ) , ( C 2 ) ?
A. Có đúng 2 mặt cầu phân biệt
B. Có duy nhất 1 mặt cầu
C. Có 2 hoặc 3 mặt cầu phân biệt tùy thuộc vào vị trí của (P), (Q)
D. Không có mặt cầu nào
Đáp án B.
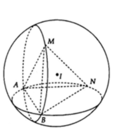
Trên hai đường tròn ( C 1 ) , ( C 2 ) lần lượt lấy M, N sao cho hai điểm này không trùng hai điểm A, B. Khi đó 4 điểm M, N, A, B không đồng phẳng nên tạo thành tứ diện ABMN. Mặt cầu ( S ) đi qua ( C 1 ) , ( C 2 ) khi đó mặt (S) đi qua A, B, M, N
Do đó có duy nhất 1 mặt cầu