Các câu hỏi tương tự
Cho hai điểm
M
1
;
3
;
1
,
N
5
;
6
;
2
. Đường thẳng MN cắt mặt phẳng Oxz tại điểm I. Điểm I chia đoạn thẳng MN theo tỉ số A.
1
2
B. 1 C. -1 ...
Đọc tiếp
Cho hai điểm M 1 ; 3 ; 1 , N 5 ; 6 ; 2 . Đường thẳng MN cắt mặt phẳng Oxz tại điểm I. Điểm I chia đoạn thẳng MN theo tỉ số
A. 1 2 B. 1 C. -1 D. - 1 2
B. 1
C. -1
D. - 1 2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x - y + z - 10 0 điểm A(1;3;2) và đường thẳng
d
:
x
-
2
+
2
t
y
1
+
t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x - y + z - 10 = 0 điểm A(1;3;2) và đường thẳng d : x = - 2 + 2 t y = 1 + t z = 1 - t . Tìm phương trình đường thẳng D cắt (P) và d lần lượt tại hai điểm M và N sao cho A là trung điểm của cạnh MN
A. x - 6 7 = y - 1 - 4 = z + 3 - 1
B. x + 6 7 = y + 1 4 = z - 3 - 1
C. x - 6 7 = y - 1 4 = z + 3 - 1
D. x + 6 7 = y + 1 - 4 = z - 3 - 1
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d tương ứng có phương trình là
2
x
-
y
+
3
z
-
3
0
và
x
+
1
-
2
y
-
2
1
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d tương ứng có phương trình là 2 x - y + 3 z - 3 = 0 và x + 1 - 2 = y - 2 1 = z + 2 - 1 . Biết đường thẳng d cắt mặt phẳng (P) tại điểm M. Gọi N là điểm thuộc d sao cho M N = 3 , gọi K là hình chiếu vuông góc của điểm N trên mặt phẳng (P). Tính độ dài đoạn MK.
A. M K = 7 105
B. M K = 7 4 21
C. M K = 4 21 7
D. M K = 105 7
Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm A(1; 5), B(‒3; 2). Biết các điểm A, B theo thứ tự là ảnh của các điểm M, N qua phép vị tự tâm O, tỉ số . Độ dài đoạn thẳng MN là A.
5
2
B. 5 C. 4 D. 10
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm A(1; 5), B(‒3; 2). Biết các điểm A, B theo thứ tự là ảnh của các điểm M, N qua phép vị tự tâm O, tỉ số . Độ dài đoạn thẳng MN là
A. 5 2
B. 5
C. 4
D. 10
Cho hình lập phương a 1 có cạnh bằng a 1. Một đường thẳng d đi qua đỉnh D và tâm I cuả mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là: A. a 1 B. a
1
2
C.
a
2
5
D.
a...
Đọc tiếp
Cho hình lập phương a = 1 có cạnh bằng a = 1. Một đường thẳng d đi qua đỉnh D ' và tâm I cuả mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là:
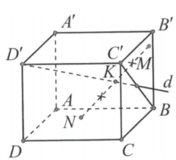
A. a =1
B. a = 1 2
C. a = 2 5
D. a = 1 3
Cho ba điểm
A
2
;
0
;
0
,
B
0
;
2
;
0
,
C
0
;
0
;
-
1
. Đường thẳng d vuông góc với (ABC) tại B cắt...
Đọc tiếp
Cho ba điểm A 2 ; 0 ; 0 , B 0 ; 2 ; 0 , C 0 ; 0 ; - 1 . Đường thẳng d vuông góc với (ABC) tại B cắt mặt phẳng (Oxz) tại điểm M. Khi đó tọa độ của M là
A. (-2;0;4)
B. (-2;0;-4)
C. (2;0;4)
D. (2;0;-4)
Khi đồ thị hàm số
y
x
3
-
3
m
x
+
2
có hai điểm cực trị A, B và đường tròn (C):
(
x
-
1
)
2
+
(
y
-
1
)
2
3
cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN A. MN...
Đọc tiếp
Khi đồ thị hàm số y = x 3 - 3 m x + 2 có hai điểm cực trị A, B và đường tròn (C): ( x - 1 ) 2 + ( y - 1 ) 2 = 3 cắt đường thẳng AB tại hai điểm phân biệt M,N sao cho khoảng cách giữa M và N lớn nhất. Tính độ dài MN
A. MN= 3
B. MN=1.
C. MN=2.
D. MN=2 3
Trong không gian Oxyz, cho đường thẳng
△
:
x
2
y
-
1
-
1
z
-
1
-
1
. Hai điểm M, N lần lượt di động trên các mặt phẳng (α): x 2; (β):z 2 sao cho trung điểm K của MN luôn thuộc đường thẳng Δ. Giá trị nhỏ nhất của độ dài MN bằng A. ...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng △ : x 2 = y - 1 - 1 = z - 1 - 1 . Hai điểm M, N lần lượt di động trên các mặt phẳng (α): x = 2; (β):z = 2 sao cho trung điểm K của MN luôn thuộc đường thẳng Δ. Giá trị nhỏ nhất của độ dài MN bằng
A. 8 5 5
B. 4 5 5
C. 3 5 5
D. 9 5 5
Trong không gian Oxyz, cho điểm M (1;2;0) và hai đường thẳng
∆
1
:
x
1
+
2
t
y
2
-
2
t...
Đọc tiếp
Trong không gian Oxyz, cho điểm M (1;2;0) và hai đường thẳng ∆ 1 : x = 1 + 2 t y = 2 - 2 t z = - 1 + t t ∈ ℝ , ∆ 2 : x = 3 + 2 s y = - 1 - 2 s z = s s ∈ ℝ . Mặt phẳng (P) đi qua M song song với trục Ox, sao cho (P) cắt hai đường thẳng ∆1; ∆2 lần lượt tại A, B thỏa mã AB =1. Khi đó mặt phẳng (P) đi qua điểm nào trong các điểm có tọa độ sau
A. F(1;3;4)
B. H(3;-2;0)
C. I(0;-2;1)
D. E(2;-3;4)


