Tham khảo:
Đặt \(a = BC,b = AC,c = AB\)
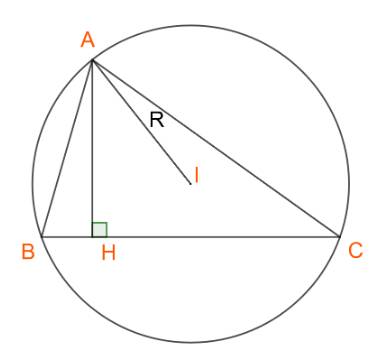
Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)
Tham khảo:
Đặt \(a = BC,b = AC,c = AB\)

Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)
a) Cho tam giác ABC không phải là tam giác vuông có \(BC = a,AC = b,AB = c\) và R là bán kính của đường trong ngoại tiếp tam giác đó. Vẽ đường kính BD.
i) Tính \(\sin \widehat {BDC}\) theo a và R.
ii) Tìm mối liên hệ giữa hai góc \(\widehat {BAC}\) và \(\widehat {BDC}\). Từ đó chứng minh rằng \(2R = \frac{a}{{\sin A}}.\)
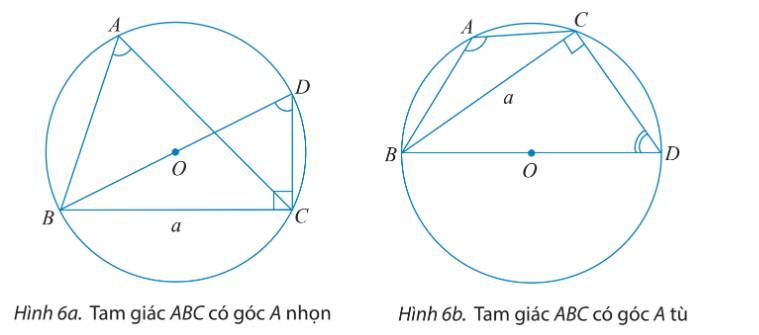
b) Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức \(2R = \frac{a}{{\sin A}}.\)
Cho tam giác ABC như Hình 10.
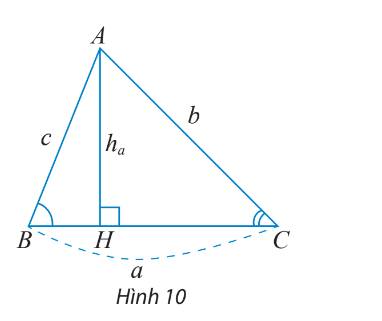
a) Viết công thức tính diện tích S của tam giác ABC theo a và \({h_a}\)
b) Tính \({h_a}\) theo b và sinC.
c) Dùng hai kết quả trên để chứng minh công thức \(S = \frac{1}{2}ab\sin C\)
d) Dùng định lí sin và kết quả ở câu c) để chứng minh công thức \(S = \frac{{abc}}{{4R}}\)
Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.
a) Chứng minh \(\frac{{{S_{BDE}}}}{{{S_{BAC}}}} = \frac{{BD.BE}}{{BA.BC}}.\)
b) Biết rằng \({S_{ABC}} = 9{S_{BDE}}\) và \(DE = 2\sqrt 2 .\) Tính \(\cos B\) và bán kính đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).
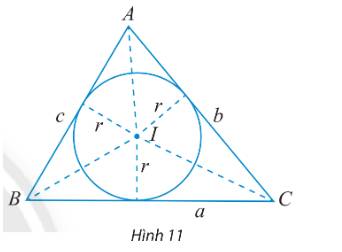
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)
Cho tam giác ABC, biết cạnh \(a = 152,\;\widehat B = {79^o},\;\widehat C = {61^o}.\) Tính các góc, các cạnh còn lại và bán kính đường tròn ngoại tiếp của tam giác đó.
Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:
a) Các cạnh \(b = 14,c = 35\) và \(\widehat A = {60^o}\)
b) Các cạnh \(a = 4,b = 5,c = 3\)
Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.
a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.
b) Tính diện tích tam giác GBC.
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và \(\widehat C \ge \widehat B.\) Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.
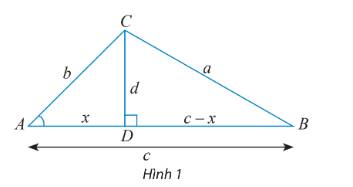
Hãy thay ? bằng các chữ cáu thích hợp để chứng minh công thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) theo gợi ý sau:
Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c - x)^2} = {d^2} + {x^2} + {c^2} - 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = \frac{?}{b} \Rightarrow ? = b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Lưu ý: Nếu \(\widehat B > \widehat C\) thì ta vẽ đường cao BD và chứng minh tương tự.
b) Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
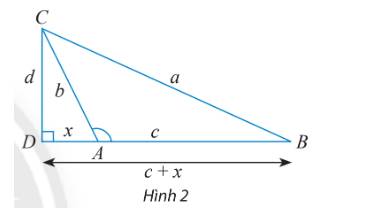
Lưu ý: Vì A là góc tù nên \(\cos A = - \frac{x}{b}.\)
c) Cho tam giác ABC vuông tại A. Hãy chứng tỏ coogn thức \({a^2} = {b^2} + {c^2} - 2bc\cos A\) có thể viết là \({a^2} = {b^2} + {c^2}.\)
Cho tam giác ABC có \(AB = 6,AC = 8\) và \(\widehat A = {60^o}.\)
a) Tính diện tích tam giác ABC.
b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.