+) Vì CE // OD (cùng vuông góc với OB) ⇒ ∠C1 = ∠O1 (so le trong)
+) Xét ΔOCE và ΔCOD có:
OC chung
∠C1 = ∠O1 ( chứng minh trên )
∠OEC = ∠ODC = 90º
Suy ra: ΔOCE = ΔCOD (cạnh huyền – góc nhọn) ⇒ CE = OD.

+) Vì CE // OD (cùng vuông góc với OB) ⇒ ∠C1 = ∠O1 (so le trong)
+) Xét ΔOCE và ΔCOD có:
OC chung
∠C1 = ∠O1 ( chứng minh trên )
∠OEC = ∠ODC = 90º
Suy ra: ΔOCE = ΔCOD (cạnh huyền – góc nhọn) ⇒ CE = OD.
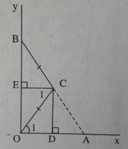
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Gọi D, E theo thứ tự là trung điểm của OA, OB. Đường vuông góc với OA tại D và đường vuông góc với OB tại E cắt nhau ở C. Chứng minh rằng: CE ⊥ CD
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Gọi D, E theo thứ tự là trung điểm của OA, OB. Đường vuông góc với OA tại D và đường vuông góc với OB tại E cắt nhau ở C. Chứng minh rằng: CA // DE
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Gọi D, E theo thứ tự là trung điểm của OA, OB. Đường vuông góc với OA tại D và đường vuông góc với OB tại E cắt nhau ở C. Chứng minh rằng: CA = CB
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Gọi D, E theo thứ tự là trung điểm của OA, OB. Đường vuông góc với OA tại D và đường vuông góc với OB tại E cắt nhau ở C. Chứng minh rằng: Ba điểm A, B, C thẳng hàng
Cho góc vuông xOy điểm A thuộc tia Ox điểm B thuộc tia Oy . Gọi D, E theo thứ tự là trung điểm của OA và OB , Đường vuông góc OA tại D và đường vuông góc OB tạiE cắt nhau ở C . CMR
a CE=OD
b CE vuông CD
c CA=CB
d CA song song DE
e ba điểm ABC thẳng hàng
Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng:
CE = OD
Cho góc tù xOy, lấy điểm A thuộc tia Ox, lấy điểm B thuộc tia Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở C. Gọi D là giao điểm của tia CB và tia đối của tia Ox, gọi E là giao điểm của tia CA và tia đối của tia Oy. Chứng minh rằng:
a) OC là tia phân giác của góc xOy?
b) tam giác ODE là tam giác cân?
c) CO vuông góc với DE?
cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. đường trung trực của đoạn thẳng OA cắt Ox tại D, đường trung trực của đoạn thẳng OB cắt Oy tại E. Gọi C là giao điểm của hai đường trung trực đó. chứng minh:
a) CE=OD
b) CEvuông góc với OD
c) CA=CB
d) CA//DE
cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. đường trung trực của đoạn thẳng OA cắt Ox tại D, đường trung trực của đoạn thẳng OB cắt Oy tại E. Gọi C là giao điểm của hai đường trung trực đó. chứng minh:
a) CE=OD
b) CEvuông góc với OD
c) CA=CB
d) CA//DE