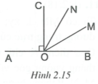
Ta có
O
C
⊥
A
B
nên
A
O
C
^
=
B
O
C
^
=
90
°
(1)
Tia OC nằm giữa hai tia OA, OB. (2)
Từ (1) và (2) suy ra tia OC là tia phân giác của góc AOB.
Ta có B O M ^ = C O N ^ = 1 3 B O C ^ = 30 ° .
Tia ON nằm trong góc BOC nên B O N ^ + C O N ^ = B O C ^ .
Suy ra B O N ^ = 90 ° − 30 ° = 60 ° .
Tia OM nằm giữa hai tia OB, ON. (3)
Do đó B O M ^ + M O N ^ = B O N ^ ⇒ M O N ^ = 60 ° − 30 ° = 30 ° .
Vậy B O M ^ = M O N ^ = C O N ^ = 30 ° (4)
Từ (3) và (4) suy ra tia OM là tia phân giác của góc BON.
Tia ON nằm giữa hai tia OM và OC (5)
Từ (4) và (5) suy ra tia ON là tia phân giác của góc COM.
Tóm lại, các tia OC, OM, ON lần lượt là các tia phân giác của các góc AOB, BON và COM.