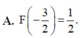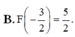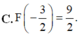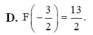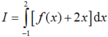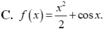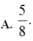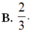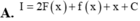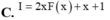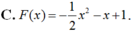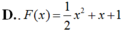\(f\left(x\right)=\left|2x-3\right|=\left[{}\begin{matrix}2x-3\left(x\ge\dfrac{3}{2}\right)\\-2x+3\left(x< \dfrac{3}{2}\right)\end{matrix}\right.\)
\(\Rightarrow F\left(x\right)=\left[{}\begin{matrix}\int\left(2x-3\right)dx=x^2-3x+C_1\left(x\ge\dfrac{3}{2}\right)\\\int\left(-2x+3\right)dx=-x^2+3x+C_2\left(x< \dfrac{3}{2}\right)\end{matrix}\right.\)
\(F\left(2\right)=4\Leftrightarrow2^2-3.2+C_1=4\Leftrightarrow C_1=6\)
\(\Rightarrow F\left(x\right)=x^2-3x+6\left(x\ge\dfrac{3}{2}\right)\)
\(\Rightarrow F\left(4\right)=4^2-3.4+6=10\)
Để Hs \(F\left(x\right)\) liên tục tại \(x=\dfrac{3}{2}\) khi và chỉ khi
\(\Leftrightarrow\lim\limits_{x\rightarrow\dfrac{3}{2}^+}F\left(x\right)=\lim\limits_{x\rightarrow\dfrac{3}{2}^-}F\left(x\right)\)
\(\Leftrightarrow\left(\dfrac{3}{2}\right)^2-3.\dfrac{3}{2}+6=-\left(\dfrac{3}{2}\right)^2+3.\dfrac{3}{2}+C_2\)
\(\Leftrightarrow C_2=6\)
\(\Rightarrow F\left(x\right)=-x^2+3x+6\left(x< \dfrac{3}{2}\right)\)
\(\Rightarrow F\left(-1\right)=-\left(-1\right)^2+3.\left(-1\right)+6=2\)
Vậy \(2F\left(-1\right)+F\left(4\right)=2.2+10=14\)