Các câu hỏi tương tự
nếu 0<a<b<c<d<e<f
(a-b)(c-d)(e-f).x=(b-a)(d-c)(f-e) thì x=...
Cho hàm số f(x) có đạo hàm liên tục trên R thảo mãn
x
.
f
x
-
x
2
.
e
x
f
x
và f(1) e. Tính tích phân
I
∫
1
2
f
x
d
x
A.
I
e
2...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên R thảo mãn x . f ' x - x 2 . e x = f x và f(1) = e. Tính tích phân I = ∫ 1 2 f x d x
A. I = e 2 - 2 e
B. I = e
C. I = e 2
D. I = 3 e 2 - 2 e
Cho 2 đường thẳng
d
1
:
x
2
y
-
1
1
z
+
1
-
1
,
d
2
:
x...
Đọc tiếp
Cho 2 đường thẳng d 1 : x 2 = y - 1 1 = z + 1 - 1 , d 2 : x = 1 + t y = - 1 - 2 t z = 2 + t . Gọi M a ; b ; c là điểm thuộc d 1 và N d , e , f là điểm thuộc d 2 sao cho MN ngắn nhất, khi đó tổng a + b + c + d + e + f bằng
A. 11 7
B. - 10 7
C. - 11 7
D. 10 7
Cho hàm số yf(x) xác định và liên tục trên [1;e] thỏa mãn
xf
(
x
)
x
[
f
(
x
)
]
2
+
3
f
(
x
)
+
4
x
và f(1) -3. Tính f(e). A.
5
2
e
B. -...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
,
(
a
,
b
,
c
,
d
,
e
∈
ℝ
)
Hàm yf(x) có bảng xét dấu như sau: Số nghiệm của phương trình f(x)e là A....
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
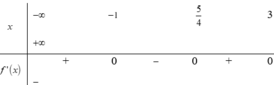
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Cho hàm số f(x) liên tục trong đoạn [1;e], biết
∫
1
e
f
(
x
)
x
d
x
1
, f(e) 2. Tích phân
∫
1
e...
Đọc tiếp
Cho hàm số f(x) liên tục trong đoạn [1;e], biết ∫ 1 e f ( x ) x d x = 1 , f(e) = 2. Tích phân ∫ 1 e f ' ( x ) ln x d x = ?
A. 1
B. 0
C. 2
D. 3
cho hình vuông ABCD cố định, độ dài cạnh là a. E là điểm di chuyển trên cạnh CD (E khác D ), đường thẳng AE cắt đường thẳng BC tại F, đường thẳng vuông góc với AE tại A cắt đường thẳng CD tạ K.1) chứng minh hai tam giác ABE và ADK bằng nhau. Suy ra tam giác AFK vuông cân.2) gọi I là trung điểm của FK. chứng minh I là đường tròn đi qua A,C,F,K và I di chuyển trên đường thẳng cố định khi E di động trên CD
Đọc tiếp
cho hình vuông ABCD cố định, độ dài cạnh là a. E là điểm di chuyển trên cạnh CD (E khác D ), đường thẳng AE cắt đường thẳng BC tại F, đường thẳng vuông góc với AE tại A cắt đường thẳng CD tạ K.
1) chứng minh hai tam giác ABE và ADK bằng nhau. Suy ra tam giác AFK vuông cân.
2) gọi I là trung điểm của FK. chứng minh I là đường tròn đi qua A,C,F,K và I di chuyển trên đường thẳng cố định khi E di động trên CD
Cho hàm số
y
f
(
x
)
2019
l
n
e
x
2019
+
e
. Tính giá trị biểu thức
A
f
’
(
1
)
+...
Đọc tiếp
Cho hàm số y = f ( x ) = 2019 l n e x 2019 + e . Tính giá trị biểu thức A = f ’ ( 1 ) + f ’ ( 2 ) + … + f ’ ( 2018 )
A. 2018
B. 1009
C. 2017 2
D. 2019 2
Cho đa thức biến x có dạng
f
x
x
4
+
2
a
x
3
+
4
b
x
2
+
8
c
x
+
16
d
a
,
b
,
c
,
d
∈
R...
Đọc tiếp
Cho đa thức biến x có dạng f x = x 4 + 2 a x 3 + 4 b x 2 + 8 c x + 16 d a , b , c , d ∈ R thỏa mãn f 4 + i = f - 1 - i = 0 . Khi đó a + b + c + d bằng
A. 34
B. 17 8
C. 17 5
D. 25 8
Cho hàm số yf(x) có đạo hàm liên tục trên R. Biết f(1)e và
(
x
+
2
)
f
(
x
)
x
f
(
x
)
-
x
3
, với mọi x thuộc R. Tính f(2). A.
4
e
2
-
4
e
+
4
B.
4...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết f(1)=e và ( x + 2 ) f ( x ) = x f ' ( x ) - x 3 , với mọi x thuộc R. Tính f(2).
A. 4 e 2 - 4 e + 4
B. 4 e 2 - 2 e + 1
C. 2 e 3 - 2 e + 2
D. 4 e 2 + 4 e - 4


