Các câu hỏi tương tự
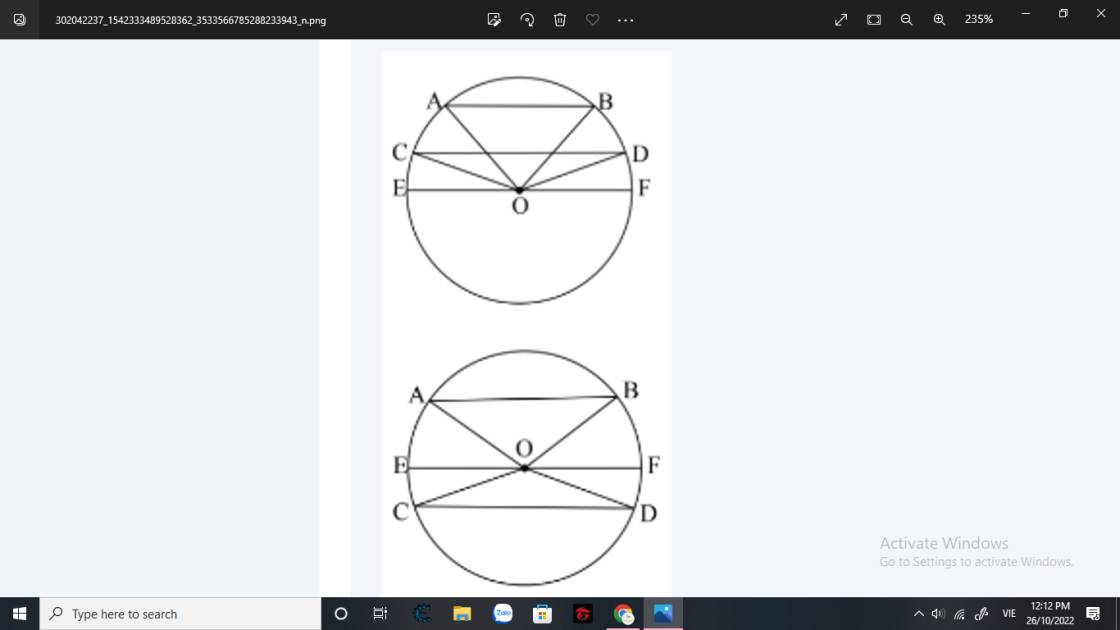
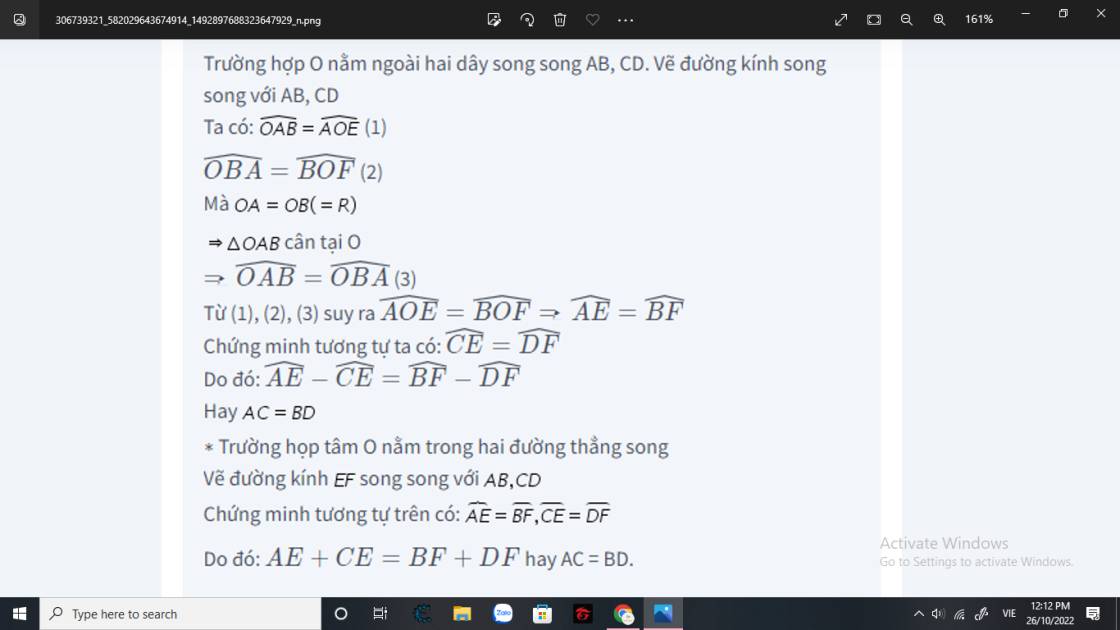
Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
cho đường tròn tâm O đường kính AB. Vẽ hai dây AM và BN song song với nhau sao cho số đo cung nhỏ BN<90. Vẽ dây MD song song với AB, dây DN cắt AB tại E.Chứng minh a,BM bằng AD b,DN AB c,DE bằng EN
Xem chi tiết
Chứng minh hai cung bị chắn bởi hai dây song song thì bằng nhau
Chứng minh rằng trong 1 đường tròn, 2 cung bị chắn bởi 2 dây song song thì bằng nhau.
Cho đường tròn (O;R) và dây cung AB cố định không đi qua tâm O; C và D là hai điểm di động trên cung lớn AB sao cho AD và BC luôn song song với nhau. Gọi M là giao điểm của AC và BD . Chứng minh rằng: 1) , suy ra AOMB là tứ giác nội tiếp. 2) 3) Đường thẳng d đi qua M và song song với AD luôn đi qua một điểm cố định.
Đọc tiếp
Cho đường tròn (O;R) và dây cung AB cố định không đi qua tâm O; C và D là hai điểm di động trên cung lớn AB sao cho AD và BC luôn song song với nhau. Gọi M là giao điểm của AC và BD . Chứng minh rằng:
1) ![]() , suy ra AOMB là tứ giác nội tiếp.
, suy ra AOMB là tứ giác nội tiếp.
2) ![]()
3) Đường thẳng d đi qua M và song song với AD luôn đi qua một điểm cố định.
Cho đường tròn (O; R) và dây AB cố định không đia qua tâm O; C và D là hai điểm di động trên cung lớn AB sao cho AD và BC luôn song song với nhau. Gọi M là giao điểm của
AC và BD. Chứng minh rằng:
a) Góc AMB bằng góc AOB, suy ra tứ giác AOMB nội tiếp.
b) OM vuông BC.
c) Đường thẳng d đi qua M và song song với AD luôn đi qua một điểm cố định.
Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB.
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:
AOC ^ = AIC ^
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:
A O C ^ = A I C ^