+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 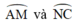
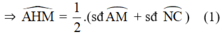
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 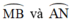
+ Do M và N là điểm chính giữa của cung A B ⏜ v à A C ⏜
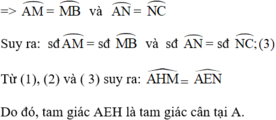

+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 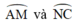
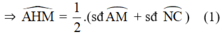
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 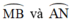
+ Do M và N là điểm chính giữa của cung A B ⏜ v à A C ⏜
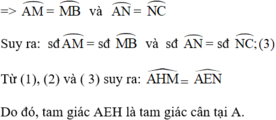
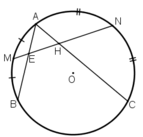
Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.
Cho (O) và hai dây AB,AC. Gọi M,N lần lượt là điểm chính giữa của \(\widebat{AB}\);\(\widebat{AC}\). đường thẳng MN cắt dây AB tại D, cắt dây AC tại E. Chứng minh tam giác ADE cân
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.
Cho nửa đường tròn tâm O, đường kính AB. Gọi C là một điểm bất kì trên nửa đường tròn đó và M là điểm chính giữa của cung AC. Dây AC cắt dây BM tại H, đường thằng AM cắt đường thẳng BC tại E. 1.Chứng minh: a.Tứ giác EMHC nối tiếp được một đường tròn. b. EH vuông góc với AB. c. tam giác ABE cân.
Cho nửa đường tròn tâm O, đường kính AB. Gọi C là một điểm bất kì trên nửa đường tròn đó và M là điểm chính giữa của cung AC. Dây AC cắt dây BM tại H, đường thằng AM cắt đường thẳng BC tại E. 1.Chứng minh: a.Tứ giác EMHC nối tiếp được một đường tròn. b. EH vuông góc với AB. c. tam giác ABE cân.
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
3) Chứng minh tứ giác BHIK là hình thoi.
Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là điểm chính giữa của cung nhỏ AB và cung nhỏ BC. Hai dây AN và CM cắt nhau tại điểm I. Dây MN cắt các cạnh AB và BC lần lượt tại các điểm H và K.
2) Chứng minh N B 2 = N K . N M .
Cho đường tròn tâm (O) với dây AB cố định không phải đường kính . Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn . M,N lần lượt là điểm chính giữa cung nhỏ AB,AC. Gọi I là giao điểm của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K
a, Cm tứ giác BMHI nội tiếp
b, Cm MK.MN=MI.MC
c, Cm tam giác AKI cân tại K và tứ giác AHIK là hình thoi
Cho nửa đường tròn tâm O, đường kính AB. Gọi C là 1 điểm bất kì trên đường kính AB. Gọi C là 1 điểm bất kì trên đường tròn đó và M là điểm chính giữa của cung AC. Dây AC cắt dây BM tại H, dg thẳng AD cắt đg thẳng BC tại E
a)Chứng minh EMHC là tứ giác nội tiếp
b)EH vuông góc AB
c) Tam giác ABE cân