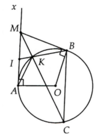
Cho đường tròn (O; R) với A là điểm cố định trên đường tròn. Kẻ tiếp tuyến Ax với (O) và lấy M là điểm bất kì thuộc tia Ax. Vẽ tiếp tuyế thứ hai MB với đường tròn (O). Gọi I là trung điểm MA, K là giao điểm của BI với (O)
a, Chứng minh các tam giác IKA và IAB đồng dạng. Từ đó suy ra tam giác IKM đồng dạng với tam giác IMB
b, Giả sử MK cắt (O) tại C. Chứng minh BC song song MA
a, ∆IAK:∆IBA => I A I B = I K I A
Mà IA = IM => I M I B = I K I M
=> ∆IKM:∆IMB
b, Chứng minh được: I M K ^ = K C B ^ => BC//MA(đpcm)

