Cho đường tròn (O; R) và dây BC cố định không đi qua tâm. Trên tia đối của tia BC lấy điểm A (A khác B). Từ A kẻ hai tiếp tuyến AM và AN với đường tròn (O) (M và N là các tiếp điểm). Gọi I là trung điểm của BC.
3) Đường thẳng qua M và vuông góc với đường thẳng ON cắt (O) tại điểm thứ hai là P. Xác định vị trí của điểm A trên tia đối của tia BC để AMPN là hình bình hành.
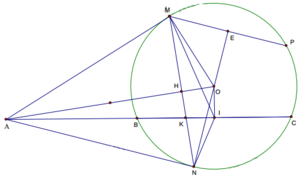
Ta có AN ⊥ NO, MP ⊥ NO, M ∉ AN => AN // MP
Do đó AMPN là hình bình hành ó AN = MP = 2x
Tam giác ∆ANO đồng dạng với ∆NEM => A N N E = N O E M = > N E = 2 x 2 R
TH 1.NE = NO – OE => 2 x 2 R = R − R 2 − x 2 ⇔ 2 x 2 = R 2 − R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 − R t ⇔ 2 t 2 − R t − R 2 = 0 ⇔ 2 t = − R t = R
Do t ≥ 0 ⇒ t = R ⇔ R 2 − x 2 = R ⇔ x = 0 ⇒ A ≡ B (loại)
TH 2 NE = NO + OE => 2 x 2 R = R + R 2 − x 2 ⇔ 2 x 2 = R 2 + R R 2 − x 2
Đặt R 2 − x 2 = t , t ≥ 0 ⇒ x 2 = R 2 − t 2 .
PTTT 2 ( R 2 − t 2 ) = R 2 + R t ⇔ 2 t 2 + R t − R 2 = 0 ⇔ 2 t = R t = − R
Do t ≥ 0 ⇒ 2 t = R ⇔ 2 R 2 − x 2 = R ⇔ x = R 3 2 = > A O = 2 R (loại)
Vậy A thuộc BC, cách O một đoạn bằng 2R thì AMPN là hbh

