Cho đường tròn (O; R) đường kính AB. Kẻ tiếp tuyến Ax, lấy P trên Ax (AP > R). Từ P kẻ tiếp tuyến PM với (O)
a, Chứng minh bôn điểm A, P, M, O cùng thuộc một đường tròn
b, Chứng minh BM // OP
c, Đường thẳng vuông góc với AB tại O cắt tia BM tại N. Chứng minh tứ giác OBNP là hình bình hành
d, Giả sử AN cắt OP tại K; PM cắt ON tại I; PN cắt OM tại J. Chứng minh I, J, K thẳng hàng
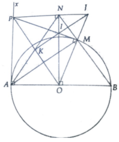
a, HS tự làm
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng

