Chọn đáp án C.
Ta có:
Góc 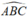 là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên:
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên:

Chọn đáp án C.
Ta có:
Góc 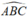 là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên:
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên:

Cho đường tròn (O; R) và dây BC. Dựng hai tiếp tuyến tại C và B cắt nhau tại A. Biết rằng B A C ^ = 60 ° . Tính AB
A. R
B. R 3
C. R 2
D. 2R
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC với B ∈ (O), C ∈ (O'). Đường vuông góc với OO' kẻ từ A cắt BC ở M
a, Tính MA theo R và r
b, Tính diện tích tứ giác BCO'O theo R và r
c, Tính diện tích ∆BAC theo R và r
d, Gọi I là trung điểm của OO'. Chứng minh rằng BC là tiếp tuyến của đường tròn (I; IM)
Cho đường tròn tâm O bán kính R, dây BC khác đường kính.Hai tiếp tuyến của đường tron (O,R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.
a) Chứng minh: AO vuông góc với BC
b) Cho biết R = 15 cm, BC = 24 cm. Tính AB, OA
c) Chứng minh: BC là tia phân giác của ^ABH.
d) Gọi I là giao điểm của AD và BH. Chứng minh IH =IB
cho đườbg tròn tâm o bán kính r co ab là 1 dây cố định(ab<2r).trên cung lớn ab lấy hai điển c,d sao cho da//bc
a>kẻ tiếp tuyến với (o;r) tại a,d;chúng cắt nhau tại i.cmr aodi nội tiếp
b)gọi m là giao điểm của ac và bd.cm m thuộc đường tròn khi c,d di chuyển trên ab.sao cho ad//bc
c>cho ab=r căn 2;bc=r.tinh s abcd theo r
cho đường tròn tâm O bán kính R đường kính AB vẽ dây BC=R đường thẳng BC cắt tiếp tuyến của (O) ở A tại D a, tính AC b, M là trung điểm AD. c/m MC là tiếp tuyến của (o) c, OM cắt AC tại I. tính AI,OI theo R
Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn ( O,R) tại B và tại C cắt nhau tại A. Kẻ đường tròn CD, kẻ BH vuông góc với CD tại H. A. Chứng minh bốn điểm A,B,O,C cùng thuộc 1 đường tròn. B. chứng minh AO vuông góc với BC. Cho biết R=15cm, BC=24cm. Tính AB,OA. C. Gọi I là giao điểm của AD và BH,E là giao điểm của BC và AC. Chứng minh IH=IB
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính: A B C ^ , B A C ^
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính: ABC ^ , BAC ^
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính: A B C ^ , B A C ^