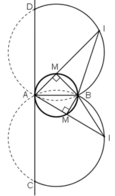
a) M ∈ đường tròn đường kính AB
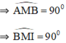
ΔBMI vuông tại M
⇒ tan I = MB / MI = 1/2
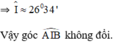
b) Dự đoán: Quỹ tích điểm I là hai cung 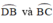 là các cung chứa góc 26º34’ dựng trên đoạn AB.
là các cung chứa góc 26º34’ dựng trên đoạn AB.
Chứng minh:
+ Phần thuận :
Theo phần a): 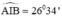 không đổi
không đổi
I nằm trên cung chứa góc 26º34’ dựng trên đoạn AB cố định
Kẻ tiếp tuyến của đường tròn tại A cắt hai cung chứa góc 26º34’ dựng trên đoạn AB tại C và D
Khi M di động trên đường tròn đường kính AB cố định thì I di động trên cung BC và BD
⇒ I nằm trên hai cung 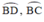 chứa góc 26º34’ dựng trên đoạn AB cố định.
chứa góc 26º34’ dựng trên đoạn AB cố định.
+ Phần đảo:
Lấy điểm I bất kỳ nằm trên hai cung 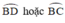 nhìn AB dưới 1 góc 26º34’.
nhìn AB dưới 1 góc 26º34’.
AI cắt đường tròn đường kính AB tại M.

⇒ BM /MI = tan I = 1/2.
Kết luận: Quỹ tích điểm I là hai cung 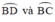 nhìn AB dưới góc 26º34’ (hình vẽ).
nhìn AB dưới góc 26º34’ (hình vẽ).
Kiến thức áp dụng
+ Trong một tam giác vuông, tan α = cạnh đối / cạnh huyền.

