Các câu hỏi tương tự
Tổng giá trị m, n để đường thẳng
(
D
)
:
x
3
+
4
t
y
1
-
4
t
(
t...
Đọc tiếp
Tổng giá trị m, n để đường thẳng ( D ) : x = 3 + 4 t y = 1 - 4 t ( t ∈ R ) z = t - 3 nằm trong mặt phẳng P : m - 1 x + 2 y - 4 z + n - 9 = 0
A. 10
B. -10
C. -8
D. 7
Trong không gian tọa độ Oxyz cho đường thẳng
d
:
x
-
1
+
t
y
1
+
t
z...
Đọc tiếp
Trong không gian tọa độ Oxyz cho đường thẳng d : x = - 1 + t y = 1 + t z = 1 - t , t ∈ R và mặt phẳng α : m 2 x - 3 y + z + 3 m = 0 (với m là tham số). Tìm tất cả giá trị của tham số m để đường thẳng d song song với mặt phẳng α
A. -2
B. 2 hoặc -2
C. 2
D. 1 hoặc 2
Trong không gian Oxyz, cho hai đường thẳng
d
:
x
1
+
t
y
2
-
t
z...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 - t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d, d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x - 1 - 2 = y - 2 1 = z 3
B. x - 4 - 2 = y - 1 = z - 2 3
C. x 2 = y - 3 - 1 = z + 1 - 3
D. x - 2 - 2 = y - 1 1 = z - 1 3
Trong không gian Oxyz, cho đường thẳng
Δ
:
x
1
+
3
t
,
y...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng Δ : x = 1 + 3 t , y = 2 t , z = 3 + t (t∈R). Một vectơ chỉ phương của Δ có tọa độ là
A. (-3;-2;-1).
B. (1;2;3).
C. (3;2;1).
D. (1;0;3).
Trong không gian Oxyz, cho đường thẳng
Δ
1
:
x
-
8
2
y
+
2
4
z
-...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng Δ 1 : x - 8 2 = y + 2 4 = z - 3 m - 1 và Δ 2 : y = 3 - t z = 2 + 2 t x = 4 + 4 t . Giá trị của m để Δ 1 và Δ 2 cắt nhau là
A. m= - 25 8
B. m= 25 8
C. m= 3.
D. m= -3
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng
∆
:
x
1
+
t
y...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng ∆ : x = 1 + t y = 2 - t z = 1 - 3 t . Phương trình của d là
A. x = t y = 3 t z = - t
B. x = t y = - 3 t z = - t
C. x 1 = y 3 = z - 1
D. x = 0 y = - 3 t z = t
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-
2
1
,
d
:
x
-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d '; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng ∆ thay đổi trên (P) nhưng luôn đi qua H đồng thời ∆ cắt d và d ' lần lượt là B, B '. Hai đường thẳng AB, A'B' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính T= a+b
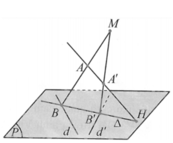
A. T = 8
B. T = 9
C. T = - 9
D. T = 6
Tổng giá trị m, n để đường thẳng
(
D
)
:
x
ư
3
+
4
t
y
1
-
4
y...
Đọc tiếp
Tổng giá trị m, n để đường thẳng ( D ) : x ư 3 + 4 t y = 1 - 4 y ( t ∈ ℝ ) z = t - 3 nằm trong mặt phẳng
( P ): ( m - 1 )x + 2y - 4z + n - 9 = 0 là:
A. 10
B. -10
C. -8
D. 7
Cho m
≠
0 và hai đường thẳng
d
:
x
-
1
m
y
-
3
1
z
+
5
m
;
∆
:
x
t...
Đọc tiếp
Cho m ≠ 0 và hai đường thẳng
d : x - 1 m = y - 3 1 = z + 5 m ; ∆ : x = t + 5 y = 2 y + 3 z = - t + 3
Nếu d cắt ∆ thì giá trị của m như thế nào trong các trường hợp dưới đây?
A. Một số nguyên dương
B. Một số nguyên âm
C. Một số hữu tỉ dương
D. Một số hữu tỉ âm



