Cho đoạn thẳng AB = 4cm. Vẽ các đường tròn (A;3cm) và (B;3cm). Đường tròn (A;3cm) cắt tia đối của tia AB tại điểm M, cắt đoạn thẳng AB tại điểm N. Đường tròn (B;3cm) cắt tia đối của tia BA tại Q và cắt đoạn thẳng BA tại P. Chứng tỏ rằng P là trung điểm của đoạn thẳng AB và N là trung điểm của đoạn thẳng AQ.
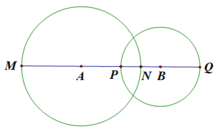
+ Đường tròn (A ;3cm) cắt tia đối của tia AB tại điểm M, cắt đoạn thẳng AB tại điểm N nên AN = AM = 3cm và điểm A nằm giữa hai điểm N và M.
Suy ra A là trung điểm của MN
=> MN = 6 cm.
+ Đường tròn (B ;3cm) cắt tia đối của tia BA tại Q, cắt đoạn thẳng BA tại P nên
BP = BQ = 2cm và B nằm giữa hai điểm P và Q. Suy ra B là trung điểm của PQ. =>PQ =4 cm.
+ Vì đường tròn (B ;3cm) cắt đoạn BA tại P nên P nằm giữa hai điểm A và B.
Suy ra A P + P B = A B ⇔ A P + 2 = 4 ⇔ A P = 2 c m
Có A P = B P = 2 cm cm nên P là trung điểm của đoạn AB.
+ Vì đường tròn (A ;3cm) cắt đoạn AB tại N nên N nằm giữa hai điểm A và B
Suy ra A N + N B = A B ⇔ 3 + N B = 4 ⇒ N B = 1 c m
Điểm Q nằm trên tia đối của tia BA nên điểm B nằm giữa hai điểm N và Q.
Suy ra N B + B Q = N Q ⇔ N Q = 2 + 1 ⇔ N Q = 3 c m
+ Lại có Q nằm trên tia đối của tia BA và NB < NQ nên điểm N nằm giữa hai điểm A và Q. Mà AN = NQ = 3cm. Suy ra N là trung điểm của PQ.

