Đáp án D
Chọn M(2;4). Phương trình tiếp tuyến tại M là: y = − 3 x + 10
Giao với tiệm cận đứng B(1;7). Giao với tiệm cận ngang C(3:1)
Giao 2 tiệm cận A(1;1)
Diện tích tam giác: S = 1 2 A B . A C = 6
Đáp án D
Chọn M(2;4). Phương trình tiếp tuyến tại M là: y = − 3 x + 10
Giao với tiệm cận đứng B(1;7). Giao với tiệm cận ngang C(3:1)
Giao 2 tiệm cận A(1;1)
Diện tích tam giác: S = 1 2 A B . A C = 6
Cho hàm số có đồ thị (C): 2 x + 1 x - 1 . Gọi M là điểm bất kì thuộc đồ thị (C). Gọi tiếp tuyến của đồ thị (C) tại M cắt các tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ (với I là giao điểm của hai đường tiệm cận của (C)). Diện tích tam giác GPQ là
A. 2
B. 4
C. 2/3
D. 1
Cho hàm số y = 2 x - 1 x - 2 có đồ thị (C). Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến ∆ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến ∆ của (C) tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào?
A. (26;27).
B. (29;30).
C. (27;28).
D. (28;29).
Cho hàm số y = 2 x - 1 x - 2 có đồ thị C . Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến ∆ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến ∆ của (C) tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào ?
A. 29 ; 30
B. 27 ; 28
C. 26 ; 27
D. 28 ; 29
Cho hàm số y = 2 x − 1 x − 2 có đồ thị (C) Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến Δ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến của Δ của (C)tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào
A. (27;28)
B. (28;29)
C. (26;27)
D. (29;30)
Cho hàm số y = x - 3 x + 1 có đồ thị (C) và một điểm A ∈ C . Tiếp tuyến với đồ thị tại A tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất bằng bao nhiêu
A. 2 + 2 2
B. 4 - 2 2
C. 3 - 2
D. 4 + 2 2
Tiếp tuyến của đồ thị hàm số y = x − 3 x + 1 C cùng với hai tiệm cận tạo thành một tam giác có diện tích bằng
A. 5
B. 8
C. 7
D. 6
Cho hàm số y = 2 x + 1 x + 1 có đồ thị C . Tiếp tuyến tại M x 0 ; y 0 x 0 < 0 của đồ thị C tạo với hai đường tiệm cận của đồ thị C một tam giác có bán kính đường tròn nội tiếp lớn nhất. Giá trị biểu thức T = 2018 x 0 + 2019 y 0 bằng
A. T = 2021
B. T = 2016
C. T = 2018
D. T = 2019
Gọi(T) là tiếp tuyến của đồ thị y = x + 1 x + 2 C tại điểm có tung độ dương, đồng thời (T)cắt hai tiệm của (C) lần lượt tại A và B sao cho độ dài AB nhỏ nhất. Khi đó (T) tạo với hai trục tọa độ một tam giác có diện tích bằng bao nhiêu?
A. 0,5
B. 2,5
C. 12,5
D. 8
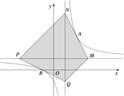
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng
A. 16.
B. 32.
C. 8.
D. 4.