Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM. Đặt MA = a, MB = b. Tính ME, MF theo a và b.
A. M E = a b b + a ; M F = a b + a
B. M E = M F = a b b + a
C. M E = b b + a ; M F = a b + a
D. M E = M F = a − b b + a
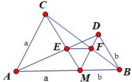
Vì các tam giác AMC và BMD đều nên B M D ^ = M A C ^ = 90 ° (vì hai góc ở vị trí đồng vị) => MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có M E E C = M D A C = b a
Suy ra
M E E C = b a ⇒ M E M E + E C = b b + a ⇒ M E a = b b + a ⇒ M E = a b b + a
Tương tự MF = b a a + b
Vậy M E = M F = a b b + a
Đáp án: B

