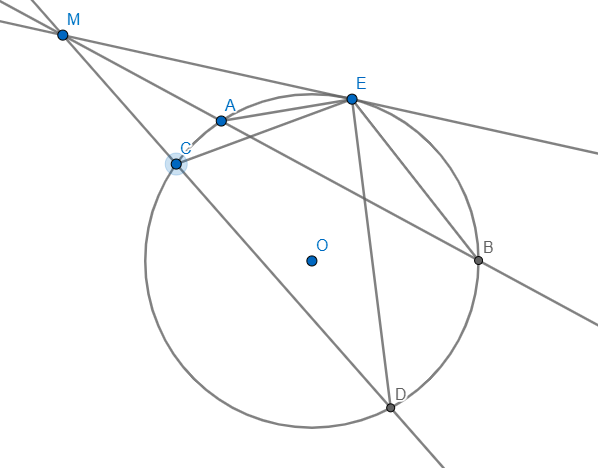
Vẽ tiếp tuyến ME
Xét \(\Delta MEA\) và \(\Delta MBE:\) Ta có: \(\left\{{}\begin{matrix}\angle MEA=\angle MBE\\\angle BMEchung\end{matrix}\right.\)
\(\Rightarrow\Delta MEA\sim\Delta MBE\left(g-g\right)\Rightarrow\dfrac{ME}{MB}=\dfrac{MA}{ME}\Rightarrow ME^2=MA.MB\)
Xét \(\Delta MEC\) và \(\Delta MDE:\) Ta có: \(\left\{{}\begin{matrix}\angle MEC=\angle MDE\\\angle DMEchung\end{matrix}\right.\)
\(\Rightarrow\Delta MEC\sim\Delta MDE\left(g-g\right)\Rightarrow\dfrac{ME}{MD}=\dfrac{MC}{ME}\Rightarrow ME^2=MC.MD\)
\(\Rightarrow MC.MD=MA.MB\Rightarrow MC.\left(MC+CD\right)=MA.\left(MA+AB\right)\)
\(\Rightarrow MC^2+MC.CD-MA^2-MA.AB=0\)
\(\Rightarrow\left(MC-MA\right)\left(MC+MA\right)+CD\left(MC-MA\right)\left(AB=CD\right)\)
\(=\left(MC-MA\right)\left(MC+MA+CD\right)=0\) mà \(MC+MA+CD>0\)
\(\Rightarrow MC=MA\)