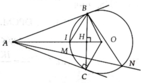
Cho điểm A nằm ngoài đường tròn (O). Qua A kẻ hai tiếp tuyến AB và AC với (O) (B, C là tiếp điểm). Kẻ cát tuyến AMN với (O) (M nằm giữa A và N)
a, Chứng minh A B 2 = A M . A N
b, Gọi H = AO ∈ BC. Chứng minh AH.AO = AM.AN
c, Đoạn thẳng AO cắt đường tròn (O) tại I. Chứng minh I là tâm đường tròn nội tiếp tam giác ABC
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

