cho điểm A nằm ngoài đường trò (O),qua a vẽ các tiếp tuyến AB,AC đến đường tròn tâm O (B,C là các tiếp điểm).
a) chứng minh tứ giác ABOC nội tiếp
b) gọi M là trung điểm của đoạn thẳng AB, gọi N là giao điểm thứ hai của đường trong (O) với MC chứng minh:MB^2=MN x MC
c) tia AN cắt đường trong (O) tại điểm thứ hai D.chứng minh:AB//CD
hình vẽ: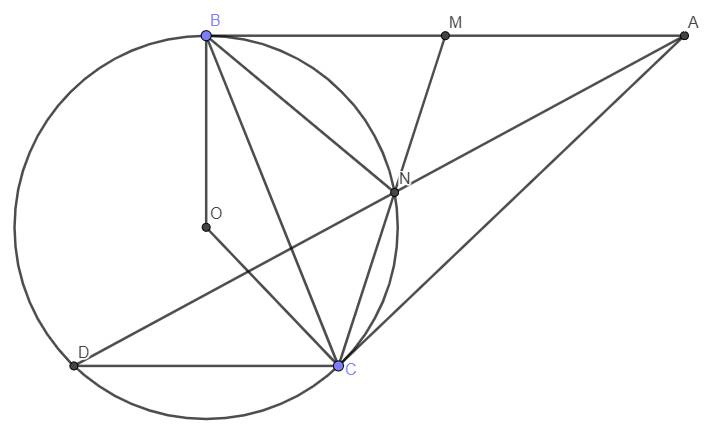
a, ta có AB, AC lần lượt là tiếp tuyến tại B và C của (O) \(\Rightarrow\left\{{}\begin{matrix}OB\perp AB\\OC\perp AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{ABO}=90^o\\\widehat{ACO}=90^o\end{matrix}\right.\)
Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=90^o+90^o=180^o\)
\(\Rightarrow\) tứ giác có tổng hai góc đối bằng \(180^o\)\(\Rightarrow\) tứ giác ABOC nội tiếp
b, Ta có: \(\widehat{MBN}=\widehat{BCN}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung chắn \(\stackrel\frown{BN}\))
Xét \(\Delta MBN\) và \(\Delta MCB\)
\(\widehat{BMN}\) chung
\(\widehat{MBN}=\widehat{BCN}\)
\(\Rightarrow\Delta MBN~\Delta MCB\left(g.g\right)\)
\(\Rightarrow BM^2=MN.MC\)
c, theo câu b, \(BM^2=MN.MC\)
mà BM=MA \(\Rightarrow MA^2=MN.MC\Rightarrow\dfrac{MA}{MC}=\dfrac{MN}{MA}\left(1\right)\)
Xét \(\Delta MAN\) và \(\Delta MCA\) có:
\(\left(1\right);\widehat{AMN}chung\)
\(\Rightarrow\Delta MAN~\Delta MCA\left(g.g\right)\)
\(\Rightarrow\widehat{MAN}=\widehat{MCA}\)
mà \(\widehat{MCA}=\widehat{ADC}\)(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung chắn \(\stackrel\frown{CN}\))
\(\Rightarrow\widehat{MAN}=\widehat{NDC}\) \(\Rightarrow\) AB//CD


