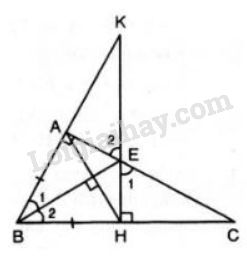
a) Xét 2 \(\Delta\) vuông \(ABE\) và \(HBE\) có:
\(\widehat{BAE}=\widehat{BHE}=90^0\left(gt\right)\)
\(\widehat{B_1}=\widehat{B_2}\) (vì \(BE\) là tia phân giác của \(\widehat{B}\))
Cạnh BE chung
=> \(\Delta ABE=\Delta HBE\) (cạnh huyền - góc nhọn)
b) Theo câu a) ta có \(\Delta ABE=\Delta HBE.\)
=> \(AE=HE\) (2 cạnh tương ứng)
Xét 2 \(\Delta\) vuông \(AEK\) và \(HEC\) có:
\(\widehat{EAK}=\widehat{EHC}=90^0\)
\(AE=HE\left(cmt\right)\)
\(\widehat{E_2}=\widehat{E_1}\) (vì 2 góc đối đỉnh)
=> \(\Delta AEK=\Delta HEC\) (2 cạnh góc vuông tương ứng bằng nhau)
=> \(EK=EC\) (2 cạnh tương ứng)
Còn câu c) thì mình đang nghĩ nhé.
Chúc bạn học tốt!
Huhu!!! Ai làm ơn làm phước trả lời giúp mình câu này đi mà ![]()

