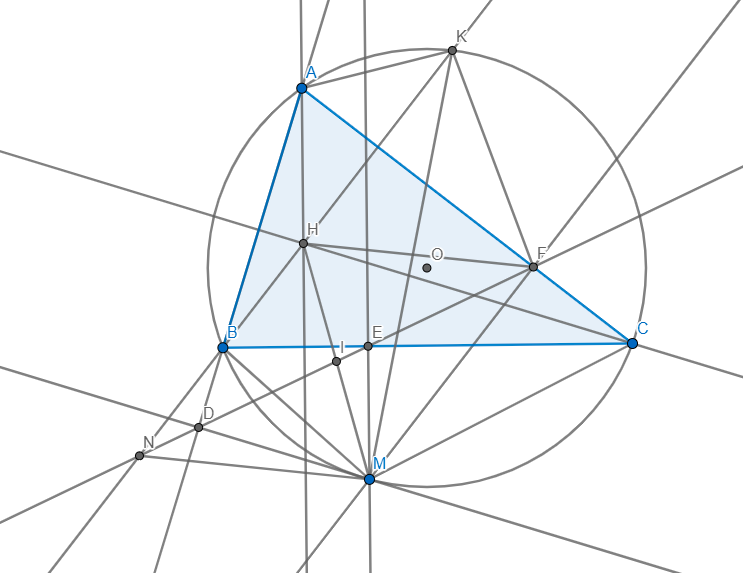
Cho DABC nhọn nội tiếp (O) (AB < AC). Gọi H là trực tâm của DABC. Đường thẳng
BH cắt (O) tại K (K khác B).
a/ Chứng minh K đối xứng với H qua AC.
b/ M là một điểm nằm trên cung nhỏ BC (M khác B và C). Gọi D, E, F lần lượt là hình
chiếu của M trên AB, BC, CA. Chứng minh 3 điểm: D, E, F thẳng hàng.
c/ Đường thẳng FD cắt đường thẳng KB và đường thẳng MH lần lượt tại N và I.
Chứng minh tứ giác MFKN nội tiếp và I là trung điểm của MH.
a) Ta có: \(\angle KAC=\angle KBC=90-\angle ACB=\angle HAC\)
mà \(AC\bot HK\Rightarrow\) H và K đối xứng với nhau qua AC
b) Ta có: \(\angle BEM+\angle BDM=90+90=180\Rightarrow BEMD\) nội tiếp
\(\Rightarrow\angle BED=\angle BMD=90-\angle DBM\)
Tương tự \(\Rightarrow MEFC\) nội tiếp \(\Rightarrow\angle FEC=\angle FMC=90-\angle MCA\)
mà \(\angle DBM=\angle MCA\) (ABMC nội tiếp)
\(\Rightarrow\angle BED=\angle CEF\) mà B,E,C thẳng hàng \(\Rightarrow D,E,F\) thẳng hàng
c) Ta có: \(\angle NKM=\angle BKM=\angle BCM=\angle EFM=\angle NFM\)
\(\Rightarrow MFKN\) nội tiếp mà \(MF\parallel NK(\bot AC)\)
\(\Rightarrow MFKN\) là hình thang cân \(\Rightarrow\angle MNH=\angle FKH=\angle FHK\) (K và H đối xứng qua AC)
\(\Rightarrow HF\parallel NM\) mà \(FM\parallel NH\) \(\Rightarrow MNHF\) là hình bình hành
có MN và HF là 2 đường chéo cắt nhau tại I
\(\Rightarrow I\) là trung điểm MH