Question

Cho ΔABC. Gọi M là trung điểm AB, D là trung điểm BC, N là điểm thuộc AC sao cho  \(\overrightarrow{CN}\) = 2\(\overrightarrow{NA}\) . K  là trung điểm MN. Chứng minh  KD = \(\dfrac{1}{4}\)\(\overrightarrow{AB}\) + \(\dfrac{1}{3}\overrightarrow{AC}\).

Answer 1

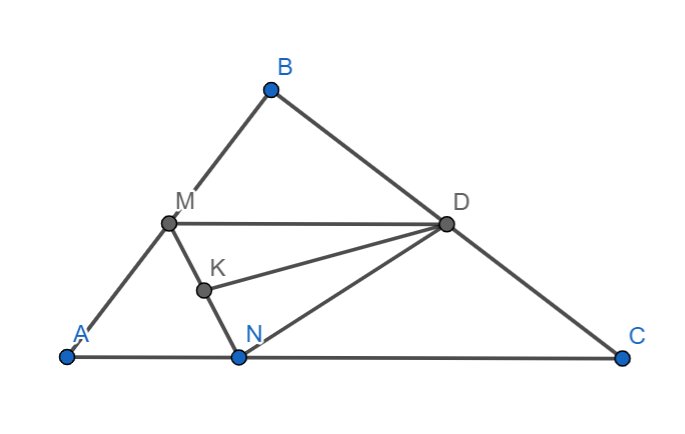
Xét \(\Delta ABC\) có:

\(M\) là trung điểm \(AB\)

\(D\) là trung điểm \(BC\)

\(\Rightarrow\) \(MD\) là đường trung bình của \(\Delta ABC\)

\(\Rightarrow\) \(MD\)\(=\)\(\dfrac{1}{2}AC\) và \(MD\) //\(AC\)

Ta có:

\(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MD}\)

\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NM}+\dfrac{1}{2}\overrightarrow{AC}\)

\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NA}+\dfrac{1}{2}\overrightarrow{AM}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{CA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\ \Rightarrow\overrightarrow{KD}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)