Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
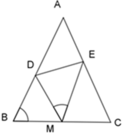
+ Ta có: D M C ^ = D M E ^ + E M C ^
Mặt khác: D M C ^ = A B C ^ + B D M ^ (góc ngoài tam giác)
Mà: D M E ^ = A B C ^ (gt) nên B D M ^ = E M C ^
+ Ta có: A B C ^ = A C B ^ (ΔABC cân tại A) và B D M ^ = E M C ^ (cmt)
=> ΔBDM ~ ΔCME (g - g)
=> B D C M = B M C E => BD.CE = CM.BM
Lại có M là trung điểm của BC và BC = 2a => BM = MC = a
=> BD.CE = a 2 không đổi
Đáp án: C
Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho D M E ^ = A B C ^ . Góc BDM bằng với góc nào dưới đây?
A. DEM
B. MDE
C. ADE
D. AED
Cho tam giác ABC cân tại A, có BC=2a. M là trung điểm BC. Lấy 2 diểm D và E theo thứ tự thuộc các cạnh AB, AC sao cho góc DME ko đổi
a. CMR BD.CE ko đổi
b. CMR CM là phân giác BCE
c. Cho tam giác ABC đều, CMR chu vi tam giác ADE ko đổi
Cho tam giác ABC cân tại A, có BC=2a, M là trung điểm BC, lấy D,E thuộc AB,AC sao cho \(\widehat{DME}=\widehat{B}\)
a) Chứng minh tích BD.CE không đổi
b) Chứng minh DM là tia phân giác của \(\widehat{BDE}\)
c) Tính C=chu vi của tam giác AED nếu tam giác ABC là tam giác đều
Cho tam giác ABC cân tại A, có cạnh BC=a. M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của góc BDE.Chứng minh rằng:
a, EM là tia phân giác của góc CED
b, Tam giác BDM đồng dạng với tam giác CME
c. BD.CE=A2
Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy D, trên cạnh AC lấy E sao cho DM là phân giáccủa góc BDE. Chứng minh rằng
a) EM là phân giác của góc CED
b) ΔBDM đồng dạng với ΔCME
c) BD.CE = a^2 (đặt MB = MC = a)
Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy D, trên cạnh AC lấy E sao cho DM là phân giáccủa góc BDE. Chứng minh rằng
a) EM là phân giác của góc CED
b) ΔBDM đồng dạng với ΔCME
c) BD.CE = a^2 (đặt MB = MC = a)
cho tam giác ABC cân ở A, BC=2a
M là trung điểm của BC, D thuộc BC, E thuộc AC sao cho góc DME=góc ABC
a, CMR BD.CE ko đổi
b, DM là phân giác góc BDE
c,nếu tam giác ABC đều cạnh =2a tính chu vi tam giác ADE
Cho tam giác ABC cân tại A , M là trung điểm của BC trên cạnh AB lấy D, AC lấy E sao cho DM là tia pg của góc BDE
Cmr:
a, EM là tia pg của góc CED
b, tam giác BDM đồng dạng tam giác CME
c, BD.CE=a^2 (a=BM)
Cho tam giác ABC cân tại A, M là trung điểm của BC. trên AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của góc BDE. CMR
a, EM là tia phân giác của góc CED
b,Tam giác BDM đồng dạng với tam giác CME
c, BD.CE = a2 (đặt MB=MC=a)
