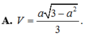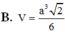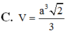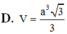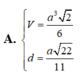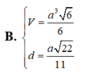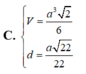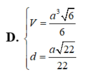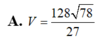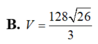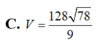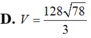Đáp án: D
Gọi độ dài cạnh đáy là x (x >0).
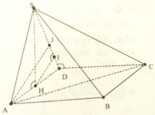
Gọi M là trung điểm của CD
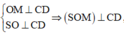

⇒ d O , ( S C D ) = O H
Ta lại có
![]()
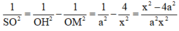
⇒ S O = a x x 2 - 4 a 2
Kết luận V S . A B C D = 1 3 x 2 . a x x 2 - 4 a 2
Thể tích khối chóp S.ABCD nhỏ nhất
⇔ f ( x ) = x 3 x 2 - 4 a 2 n h ỏ n h ấ t v ớ i x > 2 a
Lại có f ' ( x ) = 2 x 4 - 12 a 2 x 2 ( x 2 - 4 a 2 ) 3
vẽ bảng biến thiên khi đó
V S . A B C D = 1 3 ( a 6 ) 2 . a . a 6 2 a 2 = 2 3 a 3