Question

Cho bốn điểm A, B, C và D không đồng phẳng. Gọi G A ,   G B ,   G C ,   G D  lần lượt là trọng tâm của các tam giác BCD, CDA, ADB, ACB. Chứng minh rằng A G A ,   B G B ,   C G C ,   D G D  đồng qui.

Answer 1

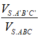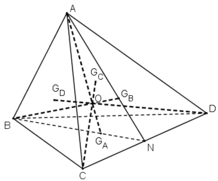
Gọi N là trung điểm CD.

+ GA là trọng tâm ΔBCD

⇒ GA ∈ trung tuyến BN ⊂ (ANB)

⇒ AGA ⊂ (ANB)

GB là trọng tâm ΔACD

⇒ GB ∈ trung tuyến AN ⊂ (ANB)

⇒ BGB ⊂ (ANB).

Trong (ANB): AGA không song song với BGB

⇒ AGA cắt BGB tại O

+ Chứng minh tương tự: BGB cắt CGC; CGC cắt AGA.

+ CGC không nằm trong (ANB) ⇒ AGA; BGB; CGC không đồng phẳng(áp dụng kết quả bài 3).

⇒ AGA; BGB; CGC đồng quy tại O

+ Chứng minh hoàn toàn tương tự: AGA; BGB; DGD đồng quy tại O

 

Vậy AGA; BGB ; CGC; DGD đồng quy tại O (đpcm).