Đáp án B
x > 0 - 1 + log 1 4 x > 0 ⇔ x > 0 log 1 4 x > 1 ⇔ x > 1 4 ⇒ m = 1 m = 4 ⇒ m + n = 5
Đáp án B
x > 0 - 1 + log 1 4 x > 0 ⇔ x > 0 log 1 4 x > 1 ⇔ x > 1 4 ⇒ m = 1 m = 4 ⇒ m + n = 5
Cho hàm số y = f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a+b+c
A. 11
B. 8
C. 10
D. 5
Biết a b (trong đó a b là phân số tối giản, a,b∈ N * ) là giá trị thực của tham số m để hàm số y = 2 x 3 - 3 mx 2 - 6 ( 3 m 2 - 1 ) x + 2018 có hai điểm cực trị x1;x2 thỏa mãn x 1 x 2 + 2 ( x 1 + x 2 ) = 1 . Tính P= a+2b.
A. P=5.
B. P=6.
C. P=7.
D. P=8.
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Xét hàm số f ( x ) = a ln x 2 + x 2 + 1 + b sin 4 x + c . 10 x Với a, b, c là những hằng số. Biết f ( log log e ) + f ( log ( ln 10 ) ) = 4 Giá trị của c nằm trong khoảng nào?
A . 1 ; 3 2
B . 0 ; 1
C . 3 2 ; 2
D . ( 2 ; 3 )
Cho hàm số y = - x + 2 x - 1 có đồ thị (C) và điểm A a ; 1 . Biết a = m n (với mọi m , n ∈ N và m n tối giản) là giá trị để có đúng một tiếp tuyến của (C) đi qua A. Khi đó giá trị m + n là:
A. 2
B. 7.
C. 5
D. 3.
Gọi m 0 là giá trị nhỏ nhất của tham số thực m để hàm số y = x 3 + 3 x 2 + m x + m nghịch biến trên một đoạn có độ dài bằng 1. Biết rằng m 0 = a b , a ∈ ℕ , b ∈ ℕ * và a b là phân số tối giản. Tính P = a b + a − b
A. P = 49
B. P = 41
C. P = 47
D. P = 36
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Cho hàm số y = f x = x 3 - 2 m - 1 x 2 + 2 - m x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a + b + c
A. a + b + c = 11
B. a + b + c = 8
C. a + b + c = 10
D. a + b + c = 5
Cho hàm số y=f(x) xác định trên tập D = ℝ \ { 1 } và liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
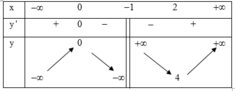
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f(x)=m-1 có hai nghiệm thực phân biệt là:
A. m < 1 m > 5
B. 1<m<5
C. m<1
D. m>5